Trong mặt phẳng với hệ trục $Oxy$, cho hình vuông \(ABCD\) có tâm là điểm \(I\). Gọi \(G\left( {1; - 2} \right)\) và \(K\left( {3;1} \right)\) lần lượt là trọng tâm các tam giác \(ACD\) và $ABI$. Biết $A\left( {a;b} \right)$ với \(b > 0\). Khi đó \({a^2} + {b^2}\) bằng
Trả lời bởi giáo viên
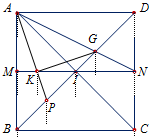
Gọi $M$, $N$ và $P$ lần lượt là các trung điểm của $AB$, $CD$ và $BI$. Ta có
\(\overrightarrow {AK} = \dfrac{2}{3}\overrightarrow {AP} \) \( = \dfrac{1}{3}\left( {\overrightarrow {AB} + \overrightarrow {AI} } \right)\) \( = \dfrac{1}{2}\overrightarrow {AB} + \dfrac{1}{6}\overrightarrow {AD} \)
\(\overrightarrow {AG} = \dfrac{2}{3}\overrightarrow {AN} \) \( = \dfrac{1}{3}\left( {\overrightarrow {AD} + \overrightarrow {AC} } \right)\) \( = \dfrac{2}{3}\overrightarrow {AD} + \dfrac{1}{3}\overrightarrow {AB} \)
\(\overrightarrow {KG} = \overrightarrow {AG} - \overrightarrow {AK} \) \( = \dfrac{1}{2}\overrightarrow {AD} - \dfrac{1}{6}\overrightarrow {AB} \).
Suy ra: \(\overrightarrow {AK} .\overrightarrow {KG} = \dfrac{1}{{12}}A{D^2} - \dfrac{1}{{12}}A{B^2} = 0\) vì \(AB = AD\) và \(\overrightarrow {AB} .\overrightarrow {AD} = 0\)
Đồng thời
\(A{K^2} = \dfrac{5}{{18}}A{B^2}\)\( = K{G^2} = \dfrac{5}{{18}}A{B^2}\). Do đó tam giác \(AKG\) vuông cân tại \(K\) nên:
\(\left\{ \begin{array}{l}\overrightarrow {AK} .\overrightarrow {KG} = 0\\A{K^2} = G{K^2}\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}2a + 3b = 9\\{\left( {3 - a} \right)^2} + {\left( {1 - b} \right)^2} = 13\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}b = \dfrac{{9 - 2a}}{3}\\13{a^2} - 78a = 0\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}b = \dfrac{{9 - 2a}}{3}\\\left[ \begin{array}{l}a = 0\\a = 6\end{array} \right.\end{array} \right.\) \( \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}a = 0\\b = 3\left( {tm} \right)\end{array} \right.\\\left\{ \begin{array}{l}a = 6\\b = - 1\left( {loai} \right)\end{array} \right.\end{array} \right.\) \( \Rightarrow {a^2} + {b^2} = 9\).
Hướng dẫn giải:
- Gọi $M$, $N$ và $P$ lần lượt là các trung điểm của $AB$, $CD$ và $BI$.
- Nhận xét tính chất của tam giác \(AKG\) rồi tìm tọa độ điểm \(A\).




