Treo một vật vào một lò xo thì nó dãn \(4cm\). Từ vị trí cân bằng, nâng vật theo phương thẳng đứng đến vị trí lò xo bị nén \(4cm\) và thả nhẹ tại thời điểm \(t = 0\) thì vật dao động điều hòa theo phương thẳng đứng trùng với trục của lò xo. Lấy \(g={\pi}^2m/s^2\). Hãy xác định thời điểm thứ \(147\) lò xo có chiều dài tự nhiên.
Trả lời bởi giáo viên
Ta có:
\(\Delta l = \dfrac{{mg}}{k} = \dfrac{g}{{{\omega ^2}}} = \dfrac{g}{{4{\pi ^2}}}{T^2} = 0,04 \to T = \sqrt {\dfrac{{4{\pi ^2}.0,04}}{{10}}} = 0,4{\rm{s}}\)
Biên độ: \(A = 8cm\)
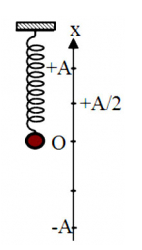
Chọn chiều dương hướng lên, ta có:
- Lò xo không biến dạng khi x = A/2
Thời điểm thứ 147 lò xo có chiều dài tự nhiên: t = t146 + t1
+ Trong 1 chu kì vật qua vị trí có chiều dài tự nhiên 2 lần \({t_{146}} = \dfrac{{146}}{2}T = 73T\)
+ Tại t = 0, vật đang ở biên +A => thời điểm ban đầu vật qua vị trí có chiều dài tự nhiên (thời gian từ A đến A/2): \({t_1} = \dfrac{T}{6}\)
=> Thời điểm thứ 147 lò xo có chiều dài tự nhiên:
\(t = {t_{146}} + {t_1} = 73T + \dfrac{T}{6} = \dfrac{{439T}}{6} \approx 29,27{\rm{s}}\)
Hướng dẫn giải:
+ Vận dụng biểu thức xác định độ dãn của lò xo treo thẳng đứng tại vị trí cân bằng: \(\Delta l = \dfrac{{mg}}{k}\)
+ Áp dụng công thức xác định thời gian lò xo qua li độ x* lần thứ n (n lẻ)
+ Sử dụng trục thời gian suy ra từ vòng tròn

