Câu hỏi:
3 năm trước
Trên mặt phẳng tọa độ \(Oxy,\) gọi \(M\) là điểm biểu diễn hình học của số phức \(z = - 1 + 2i\) và \(\alpha \) là góc lượng giác có tia đầu \(Ox,\) tia cuối \(OM.\) Tính \(\tan 2\alpha .\)
Trả lời bởi giáo viên
Đáp án đúng: d
Ta có: \(z = - 1 + 2i\) có điểm biểu diễn là \(M\left( { - 1;\,\,2} \right).\)
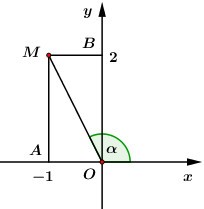
Ta có: \(\tan AOM = \dfrac{{AM}}{{OA}} = \dfrac{2}{1} = 2.\)
\( \Rightarrow \tan \alpha = - \tan AOM = - 2\) (hai góc bù nhau)
\( \Rightarrow \tan 2\alpha = \dfrac{{2\tan \alpha }}{{1 - {{\tan }^2}\alpha }} = \dfrac{{2.\left( { - 2} \right)}}{{1 - {{\left( { - 2} \right)}^2}}} = \dfrac{4}{3}\)
Hướng dẫn giải:
Cho số phức \(z = a + bi\,\,\,\left( {a,\,\,b \in \mathbb{R}} \right)\) thì \(M\left( {a;\,\,b} \right)\) là điểm biểu diễn số phức \(z.\)



