Trên mặt nước, hai nguồn kết hợp A, B cách nhau \(80cm\) luôn dao động cùng pha, có bước sóng \(6cm\). Hai điểm CD nằm trên mặt nước mà ABCD là một hình chữ nhât, \(AD = 60cm\) . Số điểm cực đại và đứng yên trên đoạn CD lần lượt là :
Trả lời bởi giáo viên
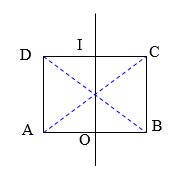
\(BD = AD = \sqrt {{{80}^2} + {{60}^2}} = 100cm\)
Do hai nguồn dao động cùng pha nên số điểm dao động với biên độ cực đại trên đoạn CD thoã mãn :
+ Số điểm cực đại trên đoạn CD thoã mãn : \(\left\{ \begin{array}{l}{d_2} - {d_1} = k\lambda \\AD - BD < {d_2} - {d_1} < AC - BC\end{array} \right.\)
Suy ra : \(AD - BD < k\lambda < AC - BC\) Hay : \(\frac{{AD - BD}}{\lambda } < k < \frac{{AC - BC}}{\lambda }\)
Hay : \(\frac{{60 - 100}}{6} < k < \frac{{100 - 60}}{6}\)
Giải ra : \( - 6,67 < k < 6,67\)
=> Kết luận có \(13\) điểm cực đại trên CD.
+ Số điểm cực tiểu trên đoạn CD thoã mãn : \(\left\{ \begin{array}{l}{d_2} - {d_1} = (2k + 1)\frac{\lambda }{2}\\AD - BD < {d_2} - {d_1} < AC - BC\end{array} \right.\)
Suy ra : \(AD - BD < (2k + 1)\frac{\lambda }{2} < AC - BC\)
Hay : \(\frac{{2(AD - BD)}}{\lambda } < 2k + 1 < \frac{{2(AC - BC)}}{\lambda }\)
Thay số :
\(\frac{{2(60 - 100)}}{6} < 2k + 1 < \frac{{2(100 - 60)}}{6}\)
Suy ra : \( - 13,33 < 2k + 1 < 13,33\)
Vậy : \( - 7,17 < k < 6,17\)
=> Kết luận có \(14\) điểm đứng yên.
Hướng dẫn giải:
Áp dụng công thức xác định cực đại trên cạnh DC của hình chữ nhật của 2 nguồn cùng pha:
\(\frac{{AD - BD}}{\lambda } < k < \frac{{AC - BC}}{\lambda }\)

