Trên mặt nước có hai nguồn sóng giống nhau A và B, hai nguồn cùng pha, cách nhau khoảng \(AB{\rm{ }} = {\rm{ }}12cm\) đang dao động vuông góc với mặt nước tạo ra sóng có bước sóng \(\lambda = 1cm\). C và D là hai điểm khác nhau trên mặt nước, CD vuông góc với AB tại M sao cho \(MA = 3cm\); \(MC = MD = 4{\rm{ }}cm\) . Số điểm dao động cực đại trên CD là:
Trả lời bởi giáo viên
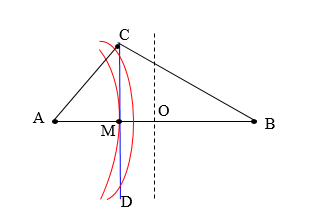
+ Ta có \(AM{\rm{ }} = 3cm\); \(BM{\rm{ }} = {\rm{ }}AB{\rm{ }}-{\rm{ }}MA{\rm{ }} = 12 - 3{\rm{ }} = 9cm\)
Và \(AM \bot MC\) => \(AC = \sqrt {A{M^2} + M{C^2}} = \sqrt {{3^2} + {4^2}} = 5cm\)
Và \(BM \bot MC\) => \(BC = \sqrt {C{M^2} + B{M^2}} = \sqrt {{4^2} + {9^2}} = 9,85cm\)
+ Xét một điểm N bất kì trên CM, điều kiện để điểm đó cực đại là : \({d_2}-{d_1} = {\rm{ }}k\lambda \)
Do hai nguồn dao động cùng pha nên :
+ Số điểm dao động với biên độ cực đại trên đoạn CM thoã mãn :\(\left\{ \begin{array}{l}{d_2} - {d_1} = k\lambda \\BC - AC \le {d_2} - {d_1} \le BM - AM\end{array} \right.\)
Ta suy ra :
\(\begin{array}{l}BC - AC \le k\lambda \le BM - AM\\ \leftrightarrow \dfrac{{BC - AC}}{\lambda } \le k \le \dfrac{{BM - AM}}{\lambda }\\ \leftrightarrow \dfrac{{9,85 - 5}}{1} \le k \le \dfrac{{9 - 3}}{1}\\ \leftrightarrow 4,85 \le k \le 6\end{array}\)
\( \to k = 5,6\)
=> Có 2 điểm cực đại.
Dễ thấy tại M là 1 cực đại nên
Trên CD có \(1.2 + 1 = 3\) cực đại
=> có 3 vị trí mà đường hyperbol cực đại cắt qua CD.
( 1 đường cắt qua CD thành 2 điểm và 1 đường qua M cắt 1 điểm)
Hướng dẫn giải:
Áp dụng công thức xác định cực đại trên cạnh DC của 2 nguồn cùng pha:
\(\frac{{BC - AC}}{\lambda } \le k \le \frac{{BM - AM}}{\lambda }\)

