Trả lời bởi giáo viên
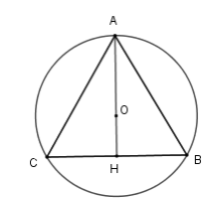
+ Gọi tam giác \(ABC\) đều cạnh \(a\) nội tiếp đường tròn \(\left( {O;2cm} \right)\) .
Khi đó \(O\) là trọng tâm tam giác \(ABC\) và \(O\) cũng là tâm đường tròn ngoại tiếp tam giác \(ABC\) nên \(AO = 2cm\) .
Gọi \(AH\) là đường trung tuyến \( \Rightarrow \dfrac{2}{3}AH = AO = 2cm \Rightarrow AH = 3cm\)
+ Theo định lý Pytago ta có \(A{H^2} = A{B^2} - B{H^2} = {a^2} - {\left( {\dfrac{a}{2}} \right)^2} = \dfrac{{3{a^2}}}{4} \Rightarrow AH = \dfrac{{a\sqrt 3 }}{2}\)
Mà \(AH = 3cm \Rightarrow 3 = \dfrac{{a\sqrt 3 }}{2} \Leftrightarrow a = \dfrac{6}{{\sqrt 3 }} = 2\sqrt 3 cm\)
Diện tích tam giác \(ABC\) là \(S = \dfrac{1}{2}AH.BC = \dfrac{1}{2}3.2\sqrt 3 = 3\sqrt 3 \left( {c{m^2}} \right)\)
Hướng dẫn giải:
+ Sử dụng tính chất tam giác đều để tìm bán kính đường tròn
+ Sử dụng định lý Pytago để tìm cạnh của tam giác đều
+ Sử dụng công thức tính diện tích tam giác \(S = \dfrac{{ah}}{2}\) với \(h\) là chiều cao ứng với cạnh đáy là \(a\)

