Câu hỏi:
2 năm trước
Tìm tất cả các giá trị của tham số m để phương trình \(\log _2^2x + {\log _2}x + m = 0\) có nghiệm \(x \in \left( {0;1} \right).\)
Trả lời bởi giáo viên
Đáp án đúng: c
Đặt \(t = {\log _2}x\). Với \(x \in \left( {0;1} \right)\) \( \Rightarrow t \in \left( { - \infty ;0} \right)\).
Khi đó phương trình trở thành \({t^2} + t + m = 0\) với \(t \in \left( { - \infty ;0} \right)\) \( \Leftrightarrow m = - {t^2} - t\,\,\forall x \in \left( { - \infty ;0} \right)\,\,\left( * \right)\)
Xét hàm số \(f\left( t \right) = - {t^2} - t\) ta có: \(f'\left( t \right) = - 2t - 1 = 0 \Leftrightarrow t = - \dfrac{1}{2} \in \left( { - \infty ;0} \right)\).
BBT:
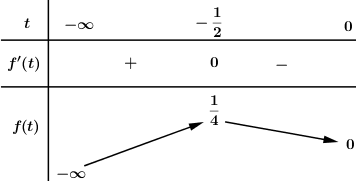
Dựa vào BBT ta thấy \(\left( * \right) \Leftrightarrow m \le \dfrac{1}{4}\).
Hướng dẫn giải:
- Đặt ẩn phụ \(t = {\log _2}x\), tìm khoảng giá trị của \(t\) ứng với \(x \in \left( {0;1} \right)\).
- Đưa phương trình về dạng phương trình bậc hai ẩn \(t\).
- Cô lập \(m\), đưa phương trình về dạng \(m = f\left( t \right)\). Lập BBT hàm số \(f\left( t \right)\) và tìm điều kiện của \(m\) để phương trình có nghiệm thỏa mãn yêu cầu bài toán.
