Tại 2 điểm A, B cách nhau \(15cm\) trên mặt nước có 2 nguồn sóng đồng bộ, tạo ra sóng mặt nước có bước sóng là \(1,2cm\). M là điểm trên mặt nước cách A và B lần lượt là \(12cm\) và \(6cm\). N đối xứng với M qua AB. Số hyperbol cực đại cắt đoạn MN là :
Trả lời bởi giáo viên
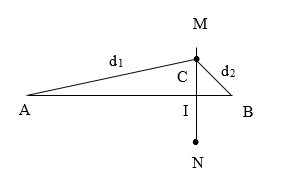
Xét điểm C trên MN:
\(\begin{array}{l}AC{\rm{ }} = {\rm{ }}{d_1}\\BC{\rm{ }} = {\rm{ }}{d_2}\end{array}\)
I là giao điểm của MN và AB
Đặt \(AI{\rm{ }} = {\rm{ }}x\), ta có:
\(\begin{array}{*{20}{l}}{A{M^2}-{\rm{ }}{x^2} = {\rm{ }}B{M^2}-{{\left( {AB - x} \right)}^2}}\\\begin{array}{l}{12^2}-{\rm{ }}{x^2} = {\rm{ }}{{\rm{6}}^2}-{\left( {15 - x} \right)^2}\\ \to x = 11,1{\rm{ }}cm\end{array}\end{array}\)
Ta có: \(11,1 \le AC = {d_1} \le 12\) (5)
C là điểm thuộc hyperbol cực đại cắt đoạn MN khi
\({d_1}-{\rm{ }}{d_2} = k\lambda = 1,2k\) (6) với k nguyên dương
Ta lại có: \(\left\{ {\begin{array}{*{20}{l}}{{d_1}^2 = {\rm{ }}{x^2} + {\rm{ }}I{C^2}}\\{{d_2}^2 = {\rm{ }}{{\left( {15-x} \right)}^2} + {\rm{ }}I{C^2}}\end{array}} \right.\)
d12 – d22 = x2 – (15 – x)2 = 108
\( \to {d_1} + {\rm{ }}{d_2} = \dfrac{{108}}{{1,2k}}\) (7)
Từ (6) và (7) \( \to {d_1} = 0,6k + \dfrac{{45}}{k}\)
\(11,1{\rm{ }} \le {\rm{ }}{d_1} = 0,6k + \dfrac{{45}}{k} \le 12\)
\(11,1 \le \dfrac{{0,6{k^2} + 45}}{k} \le 12\)
\(0,6{k^2} - 12k + 45 \le 0\) (*)
\(0,6{k^2} - 11,1k + 45 \ge 0\) (2*)
Từ (*) ta suy ra: \(5 \le k \le 15\)
Từ (2*) ta suy ra: \(k \le 6\) hoặc \(k \ge 12,5\)
Kết hợp (*) và (2*) ta suy ra: \(5 \le k \le 6\)
=> Có 2 hyperbol cực đại cắt đoạn MN.
Hướng dẫn giải:
Áp dụng điều kiện của vân cực đại của 2 nguồn cùng pha: \({d_2} - {\rm{ }}{d_1} = {\rm{ }}k\lambda \)

