Sóng truyền trên mặt nước hai điểm M và N cách nhau \(5,75\lambda \) trên cùng một phương truyền sóng. Tại thời điểm nào đó thì li độ sóng tại M và N là \({u_M} = 3mm\) đang đi lên; \({u_N} = - 4mm\). Coi biên độ sóng không đổi. Xác định biên độ sóng tại M và chiều truyền sóng.
Trả lời bởi giáo viên
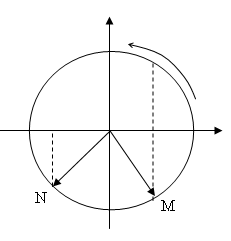
\(MN = 5\lambda + \dfrac{{3\lambda }}{4}\) suy ra xét điểm N’ gần M nhất và \(MN' = \dfrac{{3\lambda }}{4}\).
Vậy hai điểm M và N luôn dao động vuông pha với nhau.
Bài toán sóng truyền trên nhước có phương trình: \(u(t) = {u_0}\cos (2\pi ft - \dfrac{{2\pi x}}{\lambda })\) nên biên độ sóng tại các điểm M và N một lúc nào đó sẽ bằng \({u_0}\).
Tại thời điểm t: \({u_M} = 3mm;{u_N} = - 4mm\)
Do M và N dao động vuông pha với nhau nên ta có: \({\left( {\dfrac{{{u_M}}}{{{u_0}}}} \right)^2} + {\left( {\dfrac{{{u_N}}}{{{u_0}}}} \right)^2} = 1\)
\( \to {u_0} = \sqrt {u_M^2 + u_N^2} = \sqrt {{3^2} + {{\left( { - 4} \right)}^2}} = 5mm\)
Do sóng truyền theo 1 chiều nhất định nên hai điểm M và N’ sẽ lệch pha nhau \(t = \dfrac{{3\lambda }}{{4.v}} \Rightarrow \varphi = \omega .t = \omega .\dfrac{{3\lambda }}{{4.v}} = \dfrac{{2\pi .3.\lambda }}{{4.T.v}} = \dfrac{{3\pi }}{2}\)
Vậy điểm M ở dưới tại thời điểm t và căn cứ như vậy theo chiều dương thì điểm N có pha nhanh hơn điểm M là \(\dfrac{{3\pi }}{2}\) nên sóng phải truyền từ N đến M.
Hướng dẫn giải:
Sử dụng vòng tròn lượng giác và công thức tính góc quyét: $\Delta \varphi = \omega .\Delta t$

