Câu hỏi:
2 năm trước
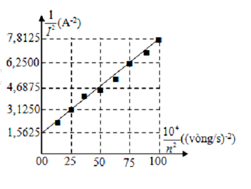
Nối hai cực của máy phát điện xoay chiều một pha vào hai đầu một cuộn dây không thuần cảm có điện trở \(r = 10\pi {\rm{ }}\Omega \) và độ tự cảm L. Biết rôto của máy phát có một cặp cực, stato của máy phát có \(20\) vòng dây và điện trở thuần của cuộn dây là không đáng kể. Cường độ dòng điện trong mạch được đo bằng đồng hồ đo điện đa năng hiện số. Kết quả thực nghiệm thu được như đồ thị trên hình vẽ. Giá trị của L là:
Trả lời bởi giáo viên
Đáp án đúng: a
Ta có : \(I = \frac{{\omega \Phi }}{{\sqrt {{r^2} + {\omega ^2}{L^2}} }} \Rightarrow \frac{1}{{{I^2}}} = \frac{{{r^2}}}{{{\omega ^2}{\Phi ^2}}} + \frac{{{L^2}}}{{{\Phi ^2}}}\)
Có : \(f = np;p = 1 = > \omega = 2\pi n;r = 10\pi \left( \Omega \right)\)
\({\rm{}} \Rightarrow \frac{1}{{{I^2}}} = \frac{{{r^2}}}{{4{\pi ^2}{n^2}{\Phi ^2}}} + \frac{{{L^2}}}{{{\Phi ^2}}} + \frac{{{{10}^4}}}{{{n^2}}} = 0 \Rightarrow \frac{1}{{{n^2}}} = 0 \Rightarrow \frac{1}{{I_0^2}} = \frac{{{L^4}}}{{{\Phi ^2}}} = 1,5625\)
+ Lại có: \(\frac{{{{10}^4}}}{{{n^2}}} = 100 \Rightarrow \frac{1}{{{n^2}}} = 0,01 \Rightarrow \frac{1}{{{I^2}}} = \frac{{{r^2}}}{{100.4{\pi ^2}{\Phi ^2}}} + \frac{{{L^2}}}{{{\Phi ^2}}} = 7,8125\) (2)
+Lấy \(\frac{{(1)}}{{(2)}} = \frac{{{L^2}}}{{\frac{{{r^2}}}{{100.4{\pi ^2}}} + {L^2}}} = \frac{{1,5625}}{{7,8125}} = \frac{1}{5} \Rightarrow L = 0,25H\)
Hướng dẫn giải:
+ Sử dụng biểu thức tính suất điện động hiệu dụng \(E = \omega {\phi _0}\)
+ Cường độ dòng điện hiệu dụng \(I = \frac{E}{Z}\)
+ Tần số của dòng điện xoay chiều \(f{\rm{ }} = {\rm{ }}np\) (n là tốc độ quay của roto ; p là số cặp cực)
Câu hỏi khác
- Bài tập các mạch điện xoay chiều có lời giải MÔN LÝ lớp 12
- Bài tập mạch RLC mắc nối tiếp có lời giải MÔN LÝ lớp 12
- Bài tập pha u,i - viết phương trình u, i có lời giải MÔN LÝ lớp 12
- Bài tập lý thuyết đại cương về dòng điện xoay chiều có lời giải MÔN LÝ lớp 12
- Bài tập đại cương dòng điện xoay chiều có lời giải MÔN LÝ lớp 12
