Một vật dao động được kích thích để dao động điều hòa với vận tốc cực đại bằng $3 m/s$ và gia tốc cực đại bằng $30\pi m/{s^2}$. Thời điểm ban đầu $t = 0$ vật có vận tốc $v=+1,5 m/s$ và thế năng đang tăng. Hỏi sau đó bao lâu vật có gia tốc bằng $ - 15\pi m/{s^2}$
Trả lời bởi giáo viên
Ta có:
\(\left\{ \begin{array}{l}{v_{{\rm{max}}}} = \omega A\\{a_{{\rm{max}}}} = {\omega ^2}A\end{array} \right. \to \left\{ \begin{array}{l}\frac{{{a_{{\rm{max}}}}}}{{{v_{{\rm{max}}}}}} = \omega = \frac{{30\pi }}{3} = 10\pi \\A = \frac{{{v_{{\rm{max}}}}}}{\omega } = \frac{3}{{10\pi }}m\end{array} \right.\)
Tại t = 0: v = +1,5m/s và thế năng đang tăng
Sử dụng hệ thức độc lập, ta có:
\({A^2} = {x^2} + \frac{{{v^2}}}{{{\omega ^2}}} \to {x^2} = {A^2} - \frac{{{v^2}}}{{{\omega ^2}}} = {\left( {\frac{3}{{10\pi }}} \right)^2} - \frac{{1,{5^2}}}{{{{\left( {10\pi } \right)}^2}}} \to x = \frac{{1,5\sqrt 3 }}{{10\pi }} = \frac{{A\sqrt 3 }}{2}\)
Khi vật có gia tốc
\(a = - 15\pi \left( {m/{s^2}} \right) = - {\omega ^2}{x_2} \to {x_2} = - \frac{{ - 15\pi }}{{{{\left( {10\pi } \right)}^2}}} = \frac{{1,5}}{{10\pi }} = \frac{A}{2}\)
=> Thời gian để vật đi từ t =0 đến vị trí có a = 15π (m/s2) là:
\(t = \frac{T}{{12}} + \frac{T}{6} = \frac{T}{4} = \frac{1}{4}\frac{{2\pi }}{\omega } = 0,05s\)
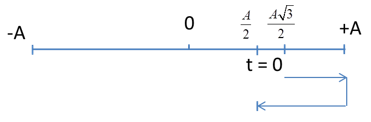
Hướng dẫn giải:
+Sử dụng công thức \(\left\{ \begin{array}{l}{v_{{\rm{max}}}} = \omega A\\{a_{{\rm{max}}}} = {\omega ^2}A\end{array} \right.\) tính chu kì và biên độ dao động của vật.
+ Sử dụng hệ thức độc lập: \({A^2} = {x^2} + \frac{{{v^2}}}{{{\omega ^2}}}\)
+ Xác định vị trí tại thời điểm t=0 (x,v)
+ Sử dụng công thức \(a = - {\omega ^2}x\)
+ Sử dụng công thức xác định chu kỳ T: \(T = \frac{{2\pi }}{\omega }\)

