Một vật có khối lượng \({m_1} = 100g\) mắc vào lò xo nhẹ có độ cứng \(k = 100N/m\), đầu kia của lò xo gắn chặt vào tường, vật và lò xo đặt trên mặt phẳng ngang không ma sát. Đặt vật thứ 2 có khối lượng \({m_2} = 300g\) sát với vật thứ nhất rồi đẩy chậm cả 2 vật cho lò xo nén lại \(10cm\). Khi thả nhẹ chúng ra, lò xo đẩy 2 vật chuyển động về 1 phía. Lấy\({\pi ^2} = 10\) , khi lò xo dãn cực đại lần đầu tiên thì 2 vật cách xa nhau một đoạn là:
Trả lời bởi giáo viên
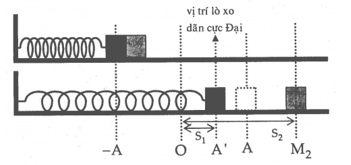
+ Đẩy chậm lò xo nén lại \(10cm\) rồi thả nhẹ ra => \(A = 10cm\)
Ta có: Tần số góc của hệ \(\omega = \sqrt {\dfrac{k}{{{m_1} + {m_2}}}} = \sqrt {\dfrac{{100}}{{0,1 + 0,3}}} = 5\sqrt {10} = 5\pi \left( {rad/s} \right)\)
+ Tại VTCB vận tốc của hệ có giá trị là \({v_{max}} = A\omega = 10.5\pi = 50\pi cm/s\) ngay sau đó vận tốc giảm dần nên vật \({m_2}\) tách ra và chuyển động thẳng đều với \(v = {v_{max}}\)
+ Khi \({m_2}\) tách ra, \({m_1}\) dao động với tần số góc \(\omega ' = \sqrt {\dfrac{k}{{{m_1}}}} = \sqrt {\dfrac{{100}}{{0,1}}} = 10\pi \left( {rad/s} \right)\) và chu kì \(T' = \dfrac{{2\pi }}{{\omega '}} = \dfrac{{2\pi }}{{10\pi }} = 0,2s\)
+ Thời gian từ lúc hai vật tách ra đến khi lò xo có độ dãn cực đại là thời gian vật \({m_1}\) đi từ VTCB ra biên mới nên mất \(\dfrac{{T'}}{4}\)
+ Quãng đường \({m_2}\) đi được trong thời gian \(\dfrac{{T'}}{4}\) là: \({S_2} = {v_{{\rm{max}}}}\dfrac{T}{4} = 50\pi .\dfrac{{0,2}}{4} = 2,5\pi cm\)
+ Khi \({m_2}\) tách ra thì \({m_1}\) dao động điều hòa với vận tốc cũ nhưng tần số góc thay đổi.
Do đó, nó dao động với biên độ: \(A' = \dfrac{{{v_{{\rm{max}}}}}}{{\omega '}} = \dfrac{{{v_{{\rm{max}}}}}}{{\sqrt {\dfrac{k}{{{m_1}}}} }} = \dfrac{{50\pi }}{{\sqrt {\dfrac{{100}}{{0,1}}} }} = 5cm\)
Quãng đường \({m_1}\) đi được trong thời gian \(\dfrac{{T'}}{4}\) là \({S_1} = A' = 5cm\)
Vậy khoảng cách giữa 2 vật khi lò xo dãn cực đại lần đầu tiên là: \(\Delta S = {S_2} - {S_1} = \left( {2,5\pi - 5} \right)cm\)

