Câu hỏi:
2 năm trước
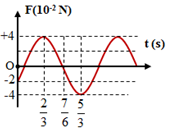
Một vật có khối lượng 100 g dao động điều hòa theo phương trình có dạng x = Acos(ωt + φ) . Biết đồ thị lực kéo về theo thời gian F(t) như hình vẽ. Lấy π2 = 10 . Phương trình vận tốc của vật là
Trả lời bởi giáo viên
Đáp án đúng: a
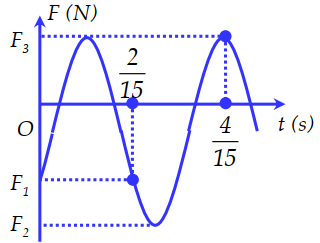
Vì F = -kx nên F biến thiên điều hòa cùng tần số ngược pha với li độ
Chu kỳ dao động là: \(T = 2.\left( {\dfrac{5}{3} - \dfrac{2}{3}} \right) = 2\,\,\left( s \right) \Rightarrow \omega = \dfrac{{2\pi }}{T} = \pi \,\,\left( {rad/s} \right)\)
Độ cứng của lò xo là: \(k = m{\omega ^2} = 0,1.{\pi ^2} = 1\,\,\left( {N/m} \right)\)
Lực kéo về cực đại là:
\({F_{kv\max }} = kA \Rightarrow {4.10^{ - 2}} = 1.A \Rightarrow A = 0,04\,\,\left( m \right) = 4\,\,\left( {cm} \right)\)
Lực kéo về ở thời điểm ban đầu là:
\({F_{kv}} = - kx \Rightarrow - {2.10^{ - 2}} = - 1.x \Rightarrow x = 0,02\,\,\left( m \right) = 2\,\,\left( {cm} \right)\)
Vậy ở thời điểm ban đầu, vật có li độ x = 2 (cm) và đang giảm
Pha ban đầu của dao động là: \(\varphi = \dfrac{\pi }{3}\,\,\left( {rad} \right)\)
Phương trình dao động là: \(x = 4\cos \left( {\pi t + \dfrac{\pi }{3}} \right)\,\,\left( {cm} \right)\)
Phương trình vận tốc của vật là:
v = x’ = \(4\pi \cos \left( {\pi t + \dfrac{\pi }{3} + \dfrac{\pi }{2}} \right) = 4\pi \cos \left( {\pi t + \dfrac{{5\pi }}{6}} \right)\,\,\left( {cm/s} \right)\)
Hướng dẫn giải:
Lực kéo về F = -kx
Vận tốc trong dao động điều hòa v = x’
Chu kỳ dao động điều hòa của con lắc lò xo \(T = 2\pi \sqrt {\dfrac{m}{k}} \)
Câu hỏi khác
- Bài tập lí thuyết dao động điều hòa có lời giải MÔN LÝ lớp 12
- Bài tập xác định thời gian vật chuyển động từ x1 đến x2, số lần qua li độ x có lời giải MÔN LÝ lớp 12
- Bài tập các đại lượng đặc trưng của DĐĐH có lời giải MÔN LÝ lớp 12
- Bài tập xác định quãng đường, tốc độ trung bình của vật trong DĐĐH có lời giải MÔN LÝ lớp 12
- Bài tập viết phương trình dao động điều hòa có lời giải MÔN LÝ lớp 12
