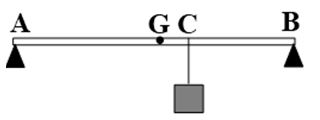
Một tấm ván đồng chất tiết diện đều, dài \(L\) được bắc qua một con mương . Bỏ qua độ dài của phần tấm ván tựa lên hai bờ mương. Một người có trọng lượng bằng trọng lượng \(P\) của tấm ván đứng trên tấm ván cách đầu A một đoạn là \(\dfrac{L}{4}\) . Hai bờ mương chịu các áp lực \({F_A}\) và \({F_B}\) lần lượt là

Một lực song song cùng chiều, có độ lớn \({F_1} = 5N,{F_2} = 15N\) đặt tại hai đầu một thanh nhẹ (khối lượng không đáng kể). AB dài \(20cm\). Hợp lực \(\overrightarrow F  = \overrightarrow {{F_1}}  + \overrightarrow {{F_2}} \) đặt cách đầu A bao nhiêu và có độ lớn bằng bao nhiêu?

Một thanh AB dài \(1m\) khối lượng \(5kg\) được đặt nằm ngang lên hai giá đỡ tại A và B. Người ta móc vào điểm C của thanh \(\left( {AC = 60cm} \right)\) một vật có khối lượng \(10kg\). Lực nén lên hai giá đỡ là \(\left( {g = 10m/{s^2}} \right)\)

Người ta đặt một thanh đồng chất \(AB = 90cm\), khối lượng \(m = 2kg\) lên một giá đỡ tại O và móc vào hai đầu A, B của thanh hai trọng vật có khối lượng \({m_1} = 4kg\) và \({m_2} = 6kg\). Vị trí O đặt giá đỡ để thanh nằm cân bằng cách đầu A

Hai người dùng một cái đòn tre để khiêng một cái hòm có trọng lượng \(500N\) như hình. Khoảng cách giữa vai của hai người là \({A_1}{A_2} = 2m\). Treo hòm vào điểm nào thì lực đè lên vai người 1 sẽ lớn hơn lực đè lên vai người 2 là \(100N\) (Bỏ qua trọng lực của đòn)

Hai người cầm hai đầu một chiếc gậy để khênh một vật nặng. Gậy có trọng lượng không đáng kể, dài \(1,4m\). Vật có trọng lượng \(700N\) được treo vào điểm C cách tay người ở đầu A của thanh \(0,6m\). Hỏi tay người ở đầu B chịu một lực bằng bao nhiêu?

Một thanh cứng có trọng lượng không đáng kể, được treo nằm ngang nhờ hai lò xo thẳng đứng có chiều dài tự nhiên bằng nhau như hình. Độ cứng của hai lò xo lần lượt là \({k_1} = 150N/m\) và \({k_2} = 100N/m\). Khoảng cách AB giữa hai lò xo là \(75cm\). Hỏi phải treo một vật nặng vào điểm C cách đầu A bao nhiêu để thanh vẫn nằm ngang?

Hai người cùng khiêng một thanh dầm bằng gỗ nặng, có chiều dài L. Người thứ hai khỏe hơn người thứ nhất. Nếu tay của người thứ nhất nâng một đầu thanh thì tay của người thứ hai phải đặt cách đầu kia của thanh một đoạn bằng bao nhiêu để người thứ hai chịu lực lớn gấp đôi người thứ nhất?