Câu hỏi:
2 năm trước
Một quả cầu nhỏ có khối lượng \(m = 1,6g\), tích điện \({q_1} = {2.10^{ - 7}}C\) được treo bằng một sợi dây tơ mảnh. Ở phía dưới nó cách \(3cm\) cần phải đặt một điện tích \({q_2}\) như thế nào để lực căng dây giảm đi một nửa.
Trả lời bởi giáo viên
Đáp án đúng: c
Ta có:
+ Khi chưa đặt điện tích, lực căng của sợi dây bằng trọng lượng của quả cầu
\(T = P = mg = \dfrac{{1,6}}{{1000}}.10 = 0,016N\)
+ Khi đặt điện tích \({q_2}\) ở dưới điện tích \({q_1}\), để lực căng dây giảm đi một nửa thì lực tương tác giữa hai điện tích phải có chiều như hình vẽ:
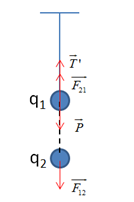
=> Tương tác giữa hai điện tích là tương tác đẩy (hai điện tích cùng dấu)
Mà \({q_1} > 0 \Rightarrow {q_2} > 0\)
\(\begin{array}{l}T' = P - {F_{21}} = \dfrac{T}{2}\\ \Rightarrow {F_{21}} = P - \dfrac{T}{2} = P - \dfrac{P}{2} = \dfrac{P}{2} = \dfrac{{0,016}}{2} = {8.10^{ - 3}}N\end{array}\)
Mặt khác, ta có: \({F_{21}} = k\dfrac{{\left| {{q_1}{q_2}} \right|}}{{{r^2}}} = {8.10^{ - 3}}N\)
Ta suy ra: \({q_2} = \dfrac{{{F_{21}}.{r^2}}}{{k{q_1}}} = \dfrac{{{{8.10}^{ - 3}}.{{\left( {0,03} \right)}^2}}}{{{{9.10}^9}{{.2.10}^{ - 7}}}} = {4.10^{ - 9}}C\)
Hướng dẫn giải:
+ Vận dụng tương tác giữa các điện tích
+ Sử dụng biểu thức tính lực tương tác giữa 2 điện tích: \(F = k\dfrac{{\left| {{q_1}{q_2}} \right|}}{{{r^2}}}\)
