Câu hỏi:
2 năm trước
Tại ba đỉnh của một tam giác đều, người ta đặt ba điện tích giông nhau \({q_1} = {q_2} = {q_3} = 2\mu C\). Cần phải đặt điện tích thứ tư \({q_0}\) tại đâu, có giá trị bằng bao nhiêu để hệ thống cân bằng.
Trả lời bởi giáo viên
Đáp án đúng: b
Vì 3 điện tích \({q_1},{\rm{ }}{q_2},{\rm{ }}{q_3}\) bằng nhau, nên nếu một điện tích cân bằng thì cả ba điện tích sẽ cân bằng
- Xét lực tác dụng lên \({q_3}\) là: \(\overrightarrow {{F_3}} = \overrightarrow {{F_{13}}} + \overrightarrow {{F_{23}}} \)
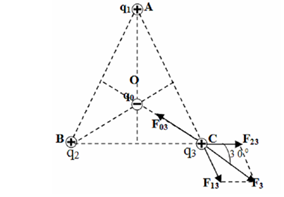
Với
\(\begin{array}{l}{F_{13}} = {F_{23}} = k\dfrac{{{q^2}}}{{{a^2}}}\\ \Rightarrow {F_3} = 2{F_{13}}{\rm{cos3}}{{\rm{0}}^0} = {F_{13}}\sqrt 3 = \dfrac{{k{q^2}}}{{{a^2}}}\sqrt 3 \end{array}\)
- Lực \(\overrightarrow {{F_3}} \) có phương là phân giác của góc C
=> Để q3 cân bằng thì cần phải có thêm lực \(\overrightarrow {{F_{03}}} \) do q0 tác dụng lên q3 sao cho \(\left\{ \begin{array}{l}\overrightarrow {{F_3}} \uparrow \downarrow \overrightarrow {{F_{03}}} \\{F_3} = {F_{03}}\end{array} \right.\)
\( \to {q_0} < 0\)
- Xét tương tự với \({q_1},{\rm{ }}{q_2},{\rm{ }}{q_3}\) thì \({q_0}\) phải nằm tại tâm của tam giác và điện tích \({q_0} < 0\):
Vậy:
\(\begin{array}{l}{F_{03}} = {F_3} = k\dfrac{{\left| {{q_0}{q_3}} \right|}}{{{{\left( {\dfrac{2}{3}\frac{{a\sqrt 3 }}{2}} \right)}^2}}} = k\dfrac{{\left| {{q_0}q} \right|}}{{{a^2}}}3\\ \Leftrightarrow k\dfrac{{\left| {{q_0}q} \right|}}{{{a^2}}}3 = k\dfrac{{{q^2}}}{{{a^2}}}\sqrt 3 \\ \Rightarrow {q_0} = - 1,15\mu C\end{array}\)
Hướng dẫn giải:
+ Áp dụng điều kiện cân bằng của vật
+ Áp dụng biểu thức định luật Cu-lông: \(F = k\dfrac{{\left| {{q_1}{q_2}} \right|}}{{{r^2}}}\)
+ Sử dụng phương pháp tổng hợp lực
+ Áp dụng hệ thức trong tam giác
