Câu hỏi:
2 năm trước
Một hình nón có bán kính đáy bằng 1, chiều cao nón bằng 2. Khi đó góc ở đỉnh của nón là 2φ thỏa mãn
Trả lời bởi giáo viên
Đáp án đúng: c
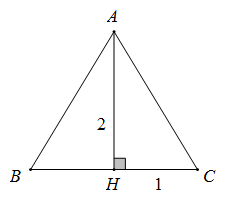
Giả sử thiết diện qua trục của hình nón đã cho là ΔABC cân tại A với A là đỉnh nón, BC là đường kính đáy của nón.
Gọi H là tâm đáy nón ⇒H là trung điểm BC,AH⊥BC
Ta có HB=HC=1,AH=2 . Ta có
2φ=∠BAC⇒φ=∠HACAC=√AH2+HC2=√5cosφ=AHAC=2√5=2√55
Hướng dẫn giải:
Góc ở đỉnh của hình nón bằng 2 lần góc tạo bởi trục và đường sinh của hình nón.