Câu hỏi:
2 năm trước
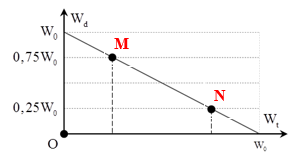
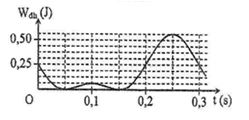
Một con lắc lò xo treo vào một điểm cố định ở nơi có gia tốc trọng trường \(g{\rm{ }} = {\rm{ }}{\pi ^2}\left( {m/{s^2}} \right)\). Cho con lắc dao động điều hoà theo phương thẳng đứng. Hình bên là đồ thị biểu diễn sự phụ thuộc của thế năng đàn hồi Wđh của lò xo vào thời gian t. Khối lượng của con lắc gần giá trị nào sau đây?
Trả lời bởi giáo viên
Đáp án đúng: d
+ Bài này đã chọn mốc thế năng tại vị trí lò xo không biến dạng.
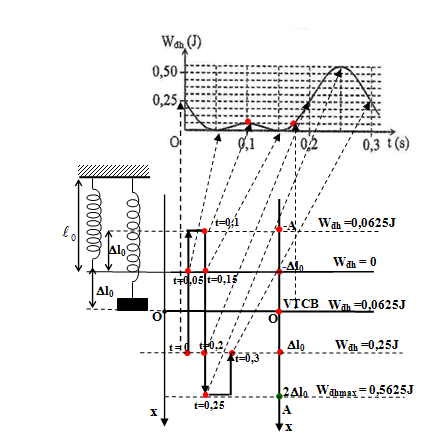
+ Từ đồ thị => Wtđh có độ chia nhỏ nhất: $0,25/4{\rm{ }} = {\rm{ }}0,0625{\rm{ }}J$
+ Tại vị trí cao nhất thế năng đàn hồi:
${W_{tdh(CN)}} = 0,0625 = \dfrac{1}{2}k{(A - \Delta {\ell _0})^2}$ (1)
+ Tại vị trí thấp nhất thế năng đàn hồi cực đại:
${W_{dh\max }} = 0,5625 = \dfrac{1}{2}k{(A + \Delta {\ell _0})^2}$(2)
+ Lấy (2) chia (1) : $9 = \dfrac{{{{(A + \Delta {\ell _0})}^2}}}{{{{(A - \Delta {\ell _0})}^2}}}$
\( \Rightarrow A = 2\Delta {\ell _0} \Rightarrow {W_{tdh(VTCB)}} = {W_{tdh(t = 0,1s)}} = 0,0625J\) (3)
+ Từ đồ thị => Chu kì dao động của con lắc: $T{\rm{ }} = {\rm{ }}0,3s$
+ Ta có: \(T = 2\pi \sqrt {\dfrac{{\Delta {\ell _0}}}{g}} \Rightarrow \Delta {\ell _0} = \dfrac{{{T^2}.g}}{{4{\pi ^2}}} = 0,025(m)\)
+ Tại VTCB: \({W_{h}} = \dfrac{1}{2}k{(\Delta {\ell _0})^2} = \dfrac{1}{2}(k.\Delta {\ell _0}).\Delta {\ell _0} = \dfrac{1}{2}m.g.\Delta {\ell _0} = 0,0625(J)\)
\( \Rightarrow \dfrac{1}{2}m.{\pi ^2}.0,025 = 0,0625 \Rightarrow m \approx 0,5629kg\)
Hướng dẫn giải:
Sử dụng lí thuyết về thế năng đàn hồi của con lắc lò xo kết hợp kĩ năng đọc đồ thị
Câu hỏi khác
- Bài tập lí thuyết dao động điều hòa có lời giải MÔN LÝ lớp 12
- Bài tập xác định thời gian vật chuyển động từ x1 đến x2, số lần qua li độ x có lời giải MÔN LÝ lớp 12
- Bài tập các đại lượng đặc trưng của DĐĐH có lời giải MÔN LÝ lớp 12
- Bài tập xác định quãng đường, tốc độ trung bình của vật trong DĐĐH có lời giải MÔN LÝ lớp 12
- Bài tập viết phương trình dao động điều hòa có lời giải MÔN LÝ lớp 12
