Câu hỏi:
2 năm trước
Một con lắc lò xo treo thẳng đứng tại nơi có gia tốc trong trường g = 10 m/s2, đầu trên lò xo gắn cố định, đầu dưới gắn với vật nặng có khối lượng m. Kích thích cho con lắc dao động điều hòa theo phương thẳng đứng với chu kì T. Khoảng thời gian lò xo bị nén trong một chu kì là \(\frac{T}{6}\) . Tại thời điểm vật đi qua vị trí lò xo không bị biến dạng thì tốc độ của vật là \(10\pi {\sqrt 3 _{}}(cm/s)\) . Lấy π2 = 10, chu kì dao động của con lắc là
Trả lời bởi giáo viên
Đáp án đúng: a
+ Độ dãn ban đầu \(\Delta {l_0} = \frac{{mg}}{k}\)
+ Ta có VTLG:
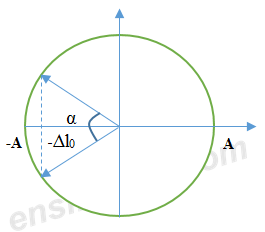
Thời gian lò xo bị nén là:
\(\begin{array}{l}
\Delta t = \frac{{2\alpha }}{{2\pi }}.T = \frac{{{\rm{arc}}\cos \frac{{\Delta {l_0}}}{A}}}{\pi }.T = \frac{T}{6} \Rightarrow {\rm{arc}}\cos \frac{{\Delta {l_0}}}{A} = \frac{\pi }{6}\\
\Leftrightarrow \frac{{\Delta {l_0}}}{A} = \frac{{\sqrt 3 }}{2} \Rightarrow \Delta {l_0} = \frac{{\sqrt 3 }}{2}.A
\end{array}\)
+ Tần số góc
\(\omega = \sqrt {\frac{k}{m}} = \sqrt {\frac{g}{{\Delta {l_0}}}} \Rightarrow \Delta {l_0} = \frac{g}{{{\omega ^2}}} = \frac{{\sqrt 3 }}{2}A \Rightarrow {\omega ^2} = \frac{{2g}}{{\sqrt 3 A}}\)
Áp dụng công thức độc lập với thời gian:
\(\begin{array}{l}
{x^2} + \frac{{{v^2}}}{{{\omega ^2}}} = {A^2} \Leftrightarrow {\left( {\frac{{\sqrt 3 }}{2}A} \right)^2} + \frac{{{v^2}}}{{{\omega ^2}}} = {A^2} \Rightarrow \frac{{{v^2}}}{{{\omega ^2}}} = \frac{1}{4}{A^2}\\
{v^2} = \frac{1}{4}{A^2}.{\omega ^2} = \frac{1}{4}{A^2}.\frac{{2g}}{{\sqrt 3 A}} = \frac{{gA}}{{2\sqrt 3 }} = {\left( {\frac{{10\sqrt 3 \pi }}{{100}}} \right)^2} \Rightarrow A = \frac{{6\sqrt 3 }}{{100}}m\\
\Rightarrow \omega = \sqrt {\frac{{2g}}{{\sqrt 3 A}}} = \sqrt {\frac{{100.2.{\pi ^2}}}{{\sqrt 3 .6\sqrt 3 }}} = \frac{{10\pi }}{3} \Rightarrow T = \frac{{2\pi }}{\omega } = 0,6s
\end{array}\)
Hướng dẫn giải:
+ Độ dãn ban đầu \(\Delta {l_0} = \frac{{mg}}{k}\)
+ Tần số góc \(\omega = \sqrt {\frac{k}{m}} \).
+ Công thức độc lập với thời gian \({x^2} + \frac{{{v^2}}}{{{\omega ^2}}} = {A^2}\)
+ Sử dụng VTLG tìm thời gian lò xo bị nén trong một chu kì.
Câu hỏi khác
- Bài tập lí thuyết dao động điều hòa có lời giải MÔN LÝ lớp 12
- Bài tập xác định thời gian vật chuyển động từ x1 đến x2, số lần qua li độ x có lời giải MÔN LÝ lớp 12
- Bài tập các đại lượng đặc trưng của DĐĐH có lời giải MÔN LÝ lớp 12
- Bài tập xác định quãng đường, tốc độ trung bình của vật trong DĐĐH có lời giải MÔN LÝ lớp 12
- Bài tập viết phương trình dao động điều hòa có lời giải MÔN LÝ lớp 12
