Câu hỏi:
2 năm trước
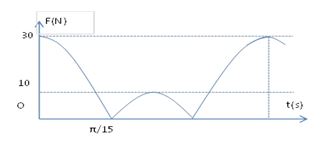
Một con lắc lò xo treo thẳng đứng tại nơi có \(g{\rm{ }} = 10m/{s^2}\) đang dao động điều hòa trên trục Ox thẳng đứng hướng lên. Cho đồ thị biểu diễn độ lớn của lực đàn hồi lò xo vào thời gian như hình vẽ. Độ cứng lò xo và khối lượng vật nặng lần lượt bằng
Trả lời bởi giáo viên
Đáp án đúng: a
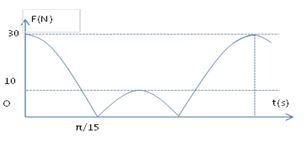
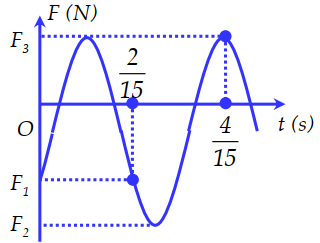
Từ đồ thị ta có:
+ \(\left\{ \begin{array}{l}{F_{dhmax}} = k\left( {A + \Delta {l_0}} \right) = 30N\,\,\,\left( 1 \right)\\{F_{dhmin}} = 0 \Rightarrow A > \Delta {l_0}\end{array} \right.\)
+ Lực đàn hồi khi vật nặng ở vị trí cao nhất là: \({F_{h}} = k(A - \Delta {l_0}) = 10N\,\,\,\,\left( 2 \right)\)
+ Thời gian từ khi lực đàn hồi của lò xo đạt giá trị cực đại đến khi lực đàn hồi của lò xo đạt giá trị cực tiểu (vị trí lò xo tự nhiên) là \(\dfrac{\pi }{{15}}s\)
Từ (1) và (2) ta có: \(\dfrac{{{\rm{A + }}\Delta {{\rm{l}}_{\rm{0}}}}}{{{\rm{A - }}\Delta {{\rm{l}}_{\rm{0}}}}} = 3 \Leftrightarrow A = 2\Delta {{\rm{l}}_{\rm{0}}}\)
Dùng đường tròn lượng giác:
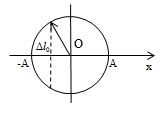
Ta có \(t = \dfrac{T}{4} + \dfrac{T}{{12}} = \dfrac{\pi }{{15}} \Rightarrow T = 0,2\pi (s) \Rightarrow \omega = 10(rad/s) \Rightarrow \left\{ \begin{array}{l}\Delta {l_0} = \dfrac{g}{{{\omega ^2}}} = \dfrac{{10}}{{{{10}^2}}} = 0,1(m)\\A = 2\Delta {l_0} = 0,2(m)\end{array} \right.\)
Thay vào (1) ta có : \(k = \dfrac{{{F_{h\max }}}}{{\Delta {l_0} + A}} = \dfrac{{30}}{{0,1 + 0,2}} = 100N/m\)
Khối lượng vật nặng: \(m = \dfrac{k}{{{\omega ^2}}} = \dfrac{{100}}{{{{10}^2}}} = 1(kg)\)
Hướng dẫn giải:
Sử dụng lí thuyết về lực đàn hồi cực đại, cực tiểu trong dao động của con lắc lò xo thẳng đứng
+ Lực đàn hồi cực đại : \({F_{d{h_{{\rm{max}}}}}} = k\left( {A + \Delta {l_0}} \right)\)
+ Lực đàn hồi cực tiểu : So sánh biên độ \(A\) và độ dãn lò xo tại vị trí cân bằng \(\Delta {l_0}\) để suy ra giá trị của lực đàn hồi cực tiểu.
Câu hỏi khác
- Bài tập lí thuyết dao động điều hòa có lời giải MÔN LÝ lớp 12
- Bài tập xác định thời gian vật chuyển động từ x1 đến x2, số lần qua li độ x có lời giải MÔN LÝ lớp 12
- Bài tập các đại lượng đặc trưng của DĐĐH có lời giải MÔN LÝ lớp 12
- Bài tập xác định quãng đường, tốc độ trung bình của vật trong DĐĐH có lời giải MÔN LÝ lớp 12
- Bài tập viết phương trình dao động điều hòa có lời giải MÔN LÝ lớp 12
