Một con lắc lò xo treo thẳng đứng, kéo vật xuống dưới theo trục của lò xo tới vị trí lò xo dãn \(7,5cm\) rồi thả nhẹ cho nó dao động điều hòa. Sau khoảng thời gian ngắn nhất \(\dfrac{π}{60} s\) thì gia tốc của vật bằng \(0,5\) gia tốc ban đầu. Lấy gia tốc trọng trường \(g = 10m/s^2\). Thời gian mà lò xo bị nén trong một chu kỳ là:
Trả lời bởi giáo viên
Chọn chiều dương hướng xuống:
Ta có:
+ Thời điểm ban đầu: x0 = +A => |a| = |amax| = ω2A
vị trí gia tốc của vật bằng nửa gia tốc ban đầu: a2 = 0,5a
Mà gia tốc tỉ lệ với li độ: a = - ω2x
=> li độ tại vị trí gia tốc của vật bằng nửa gia tốc ban đầu: x = A/2
+ Theo đề bài, ta có: thời gian vật đi từ A => A/2 là:
\(t = \frac{\pi }{{60}} = \frac{T}{6} \to T = \frac{\pi }{{10}}s\)
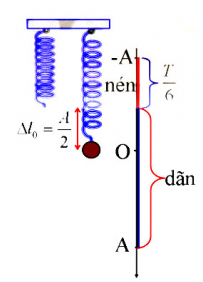
+ Độ dãn của lò xo tại VTCB:
\(\Delta l = \dfrac{{mg}}{k} = \dfrac{g}{{{\omega ^2}}} = \dfrac{g}{{4{\pi ^2}}}{T^2} = \dfrac{{10}}{{4{\pi ^2}}}{\left( {\dfrac{\pi }{{10}}} \right)^2} = 0,025m = 2,5cm\)
=> Biên độ A = 7,5 - ∆l = 7,5 - 2,5 = 5cm
=> Thời gian lò xo bị nén trong 1 chu kì:
\(t = 2\dfrac{T}{6} = \dfrac{T}{3} = \dfrac{{\dfrac{\pi }{{10}}}}{3} = \dfrac{\pi }{{30}}s\)
Hướng dẫn giải:
+ Vận dụng biểu thức tính gia tốc: \(a = -ω^2x\)
+ Áp dụng biểu thức tính độ dãn tại VTCB của lò xo treo thẳng đứng: \(\Delta l = \dfrac{{mg}}{k}\)
+ Sử dụng trục thời gian suy ra từ vòng tròn

