Một con lắc lò xo thẳng đứng gồm vật nặng khối lượng \(m = 0,8kg\) và lò xo có độ cứng $k = 160N/m$. Vật nặng được đặt trên giá đỡ nằm ngang sao cho lò xo không biến dạng. Cho giá đỡ đi xuống không vận tốc ban đầu nhanh dần đều với gia tốc \(a = \dfrac{g}{5} = 2m/{s^2}\). Chọn phương án đúng:
Trả lời bởi giáo viên
+ Khi vật A chưa rời khỏi giá đỡ B thì vật A chuyển động với gia tốc của tấm gỗ \(a = 2m/{s^2}\)
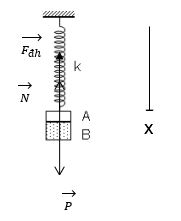
Các lực tác dụng vào vật A có khối lường m là trọng lực \(\overrightarrow P \), lực đàn hồi \(\overrightarrow {{F_{dh}}} \), phản lực \(\overrightarrow N \) do tấm gỗ tác dụng lên vật
+ Ta có, theo định luật II – Niutơn, tổng hợp các lực trên bằng tích của m và \(\overrightarrow a \)
\(\overrightarrow P + \overrightarrow {{F_{dh}}} + \overrightarrow N = m\overrightarrow a \)
+ Chiếu theo phương thẳng đứng hướng xuống dưới ta có:
\(mg - k\Delta l - N = ma\)
+ Khi vật A rời khỏi giá đỡ B thì \(N = 0\) nên \(k\Delta l = mg - ma\)
\( \to \Delta l = \dfrac{{mg - ma}}{k} = \dfrac{{0,8.10 - 0,8.2}}{{160}} = 0,04m = 4cm\)
\(\Delta l\) chính bằng quãng đường dịch chuyển vật m trước khi rời khỏi tấm gỗ.
Hướng dẫn giải:
+ Xác định chuyển động của vật, các lực tác dụng lên vật
+ Vận dụng định luật II- Niuton

