Câu hỏi:
2 năm trước
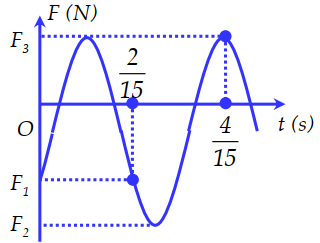
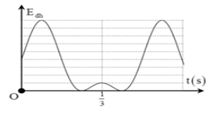
Một con lắc lò xo thẳng đứng đầu trên cố định, đầu dưới treo vật có khối lượng \(100{\rm{ }}g\). Chọn trục $Ox$ có gốc $O$ tại vị trí cân bằng, chiều dương hướng xuống dưới. Cho con lắc đó dao động điều hòa theo phương thẳng đứng thì thu được đồ thị theo thời gian của thế năng đàn hồi như hình vẽ. Lấy \(g = {\pi ^2} = 10m/{s^2}\). Vật dao động điều hòa với phương trình :
Trả lời bởi giáo viên
Đáp án đúng: b
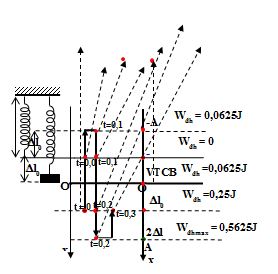
+ Thế năng đàn hồi của vật có thời điểm bằng \(0 \to A > \Delta {l_{0.}}\)
+ Thế năng đàn hồi của con lắc tại vị trí biên dương gấp 9 lần thế năng đàn hồi của con lắc tại vị trí biên âm:
\(\begin{array}{l} \to \dfrac{{{E_{d{h_{max}}}}}}{{{E_{d{h_{\min }}}}}} = {\left( {\dfrac{{A + \Delta {l_0}}}{{A - \Delta {l_0}}}} \right)^2} = 9\\ \to \left( {A + \Delta {l_0}} \right) = 3\left( {A - \Delta {l_0}} \right)\\ \to A = 2\Delta {l_0}\end{array}\)
+ Tại thời điểm \(t = 0\), ta có:
\(\dfrac{{{E_{dh}}}}{{{E_{dh\max }}}} = {\left( {\dfrac{{\Delta {l_0} + x}}{{\Delta {l_0} + A}}} \right)^2} = \dfrac{4}{9} \to x = 0,5A\), thế năng có xu hướng tăng \( \to v > 0\), vậy \({\varphi _0} = - {60^0}.\)
+ Từ thời điểm \(t = 0\) đến thời điểm \(t = \dfrac{1}{3}s\) (biên âm) tương ứng với khoảng thời gian
\(\Delta t = \dfrac{T}{6} + \dfrac{T}{2} = \dfrac{1}{3} \to T = 0,5{\rm{s}}.\)
\( \to \omega = 4\pi rad/s \to \Delta {l_0} = 6,25cm \to A = 12,5cm.\)
\( \to x = 12,5\cos \left( {4\pi t - \dfrac{\pi }{3}} \right)cm.\)
Hướng dẫn giải:
+ Vận dụng biểu thức tính lực đàn hồi : \(F = - k\left( {\Delta {l_0} + x} \right)\)
+ Sử dụng biểu thức tính lực đàn hồi cực đại : \({F_{d{h_{{\rm{max}}}}}} = k\left( {\Delta {l_0} + A} \right)\)
+ Vận dụng biểu thức tính thế năng đàn hồi
Câu hỏi khác
- Bài tập lí thuyết dao động điều hòa có lời giải MÔN LÝ lớp 12
- Bài tập xác định thời gian vật chuyển động từ x1 đến x2, số lần qua li độ x có lời giải MÔN LÝ lớp 12
- Bài tập các đại lượng đặc trưng của DĐĐH có lời giải MÔN LÝ lớp 12
- Bài tập xác định quãng đường, tốc độ trung bình của vật trong DĐĐH có lời giải MÔN LÝ lớp 12
- Bài tập viết phương trình dao động điều hòa có lời giải MÔN LÝ lớp 12
