Câu hỏi:
2 năm trước
Một con lắc lò xo nằm ngang có vật nhỏ khối lượng m dao động điều hòa với biên độ \(A\). Khi vật đến vị trí có động năng bằng thế năng thì một vật khác \(m'\) với \(\left( {m' = \dfrac{1}{2}m} \right)\) rơi thẳng đứng và dính chặt vào vật m thì khi đó 2 vật tiếp tục dao động điều hòa với biên độ:
Trả lời bởi giáo viên
Đáp án đúng: c
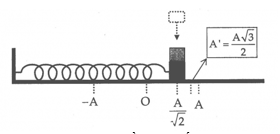
+ Động năng bằng thế năng => \(\left\{ \begin{array}{l}x = \dfrac{A}{{\sqrt 2 }}\\v = \dfrac{{{v_{{\rm{max}}}}}}{{\sqrt 2 }} = \dfrac{{\omega A}}{{\sqrt 2 }}\end{array} \right.\)
Tại đây, \(m'\) va chạm mềm với vật \(m\).
Áp dụng định luật bảo toàn động lượng theo phương ngang:
\(mv = (m + m')v' \to v' = \dfrac{{mv}}{{m + m'}} = \dfrac{{mv}}{{m + \dfrac{1}{2}m}} = \dfrac{{2v}}{3} = \dfrac{{\sqrt 2 \omega A}}{3}\)
+ Tần số góc của hệ hai vật: \(\omega ' = \sqrt {\dfrac{k}{{m + m'}}} = \sqrt {\dfrac{k}{{m + \dfrac{1}{2}}}} = \omega \sqrt {\dfrac{2}{3}} \)
Biên độ của hệ hai vật được tính từ hệ thức độc lập:
\(\begin{array}{l}A' = \sqrt {{x^2} + \dfrac{{v{'^2}}}{{\omega {'^2}}}} = \sqrt {{{\left( {\dfrac{A}{{\sqrt 2 }}} \right)}^2} + \dfrac{{\left( {\dfrac{{\sqrt 2 \omega A}}{3}} \right)}}{{{{\left( {\omega \sqrt {\frac{2}{3}} } \right)}^2}}}} \\ = \sqrt {\frac{{{A^2}}}{2} + \dfrac{{{A^2}}}{3}} = A\sqrt {\dfrac{5}{6}} \end{array}\)
Câu hỏi khác
- Bài tập lí thuyết dao động điều hòa có lời giải MÔN LÝ lớp 12
- Bài tập xác định thời gian vật chuyển động từ x1 đến x2, số lần qua li độ x có lời giải MÔN LÝ lớp 12
- Bài tập các đại lượng đặc trưng của DĐĐH có lời giải MÔN LÝ lớp 12
- Bài tập xác định quãng đường, tốc độ trung bình của vật trong DĐĐH có lời giải MÔN LÝ lớp 12
- Bài tập viết phương trình dao động điều hòa có lời giải MÔN LÝ lớp 12
