Một con lắc lò xo gồm một vật nhỏ nặng m=100g dao động điều hòa theo phương thẳng đứng với biên độ 6cm, chu kỳ \(T = \frac{\pi }{5}s\) tại nơi có g=10m/s2. Tính thời gian trong một chu kỳ, lực đàn hồi có độ lớn không nhỏ hơn 1,3N.
Trả lời bởi giáo viên
Ta có:
+ Độ cứng của con lắc lò xo:
\(k = m{\omega ^2} = m{\left( {\frac{{2\pi }}{T}} \right)^2} = 0,1{\left( {\frac{{2\pi }}{{\frac{\pi }{5}}}} \right)^2} = 10N/m\)
+ Độ dãn của lò xo tại VTCB:
\(\Delta l = \frac{{mg}}{k} = \frac{{0,1.10}}{{10}} = 0,1m = 10cm > A = 6cm\)
=> Lò xo luôn dãn
Khi lực đàn hồi bằng 1,3N thì lò xo dãn 1 đoạn ∆x:
\(\left| {{F_{dh}}} \right| = k\Delta x \to \Delta x = \frac{{\left| {{F_{dh}}} \right|}}{k} = \frac{{1,3}}{{10}} = 0,13m = 13cm\)
=> li độ của vật khi đó:
\(x = \Delta x - \Delta l = 13 - 10 = 3cm\)
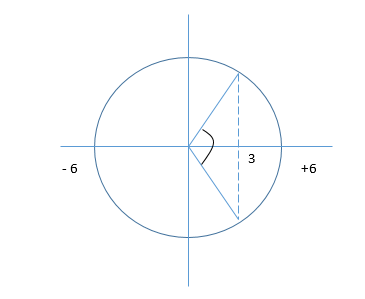
=> Bài toán tương đương với việc tìm thời gian trong một chu kì vật có li độ x ≥ 3
Từ vòng tròn lượng giác,
=> Trong 1 chu kì, thời gian vật có li độ x ≥ 3 là:
\(t = 2\frac{T}{6} = \frac{T}{3} = \frac{\pi }{{15}} \approx 0,21{\rm{s}}\)
Hướng dẫn giải:
+ Vận dụng biểu thức tính tần số góc: \(\omega = \sqrt {\frac{k}{m}} \) để tính độ cứng k
+ Áp dụng biểu thức tính độ dãn tại VTCB của lò xo treo thẳng đứng: \(\Delta l = \frac{{mg}}{k}\)
+ Áp dụng biểu thức tính lực đàn hồi: Fđh = -k. ∆x
+ Sử dụng trục thời gian suy ra từ vòng tròn

