Câu hỏi:
2 năm trước
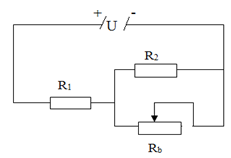
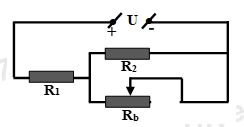
Một biến trở Rb có giá trị lớn nhất là 30Ω được mắc với hai điện trở R1 = 15Ω và R2 = 10Ω thành hai đoạn mạch có sơ đồ như hình vẽ, trong đó hiệu điện thế không đổi U = 4,5V. Hỏi khi điều chỉnh biến trở thì cường độ dòng điện chạy qua biến trở R1 có giá trị lớn nhất Imax và nhỏ nhất Imin là bao nhiêu?
Trả lời bởi giáo viên
Đáp án đúng: c
Tóm tắt:
\(\begin{array}{*{20}{l}}{{R_{bmax}}\; = 30\Omega ;{R_1}\; = 15\Omega ;{R_2}\; = 10\Omega ;U = 4,5V}\\{{I_{1max}}\; = ?;{\rm{ }}{I_{1min}}\; = ?}\end{array}\)
Cách giải:
Mạch điện gồm \({R_1}\,nt\,\left( {{R_2}//{R_b}} \right)\)
Điện trở tương đương của cụm đoạn mạch (R2 // Rb) là: \({R_{2b}}\, = \dfrac{{{R_2}{R_b}}}{{{R_2} + {R_b}}}\)
Điện trở tương đương toàn mạch: \({R_{td}}\; = {R_1}\; + {R_{2b}} = {R_1} + \dfrac{{{R_2}{R_b}}}{{{R_2} + {R_b}}}\)
Cường độ dòng điện chạy qua R1: \({I_1} = I = \dfrac{U}{{{R_{td}}\;}} = \dfrac{U}{{{R_1} + \dfrac{{{R_2}{R_b}}}{{{R_2} + {R_b}}}}}\)
+ Để \({I_{1\max }} \Leftrightarrow {R_{td\min }} \Leftrightarrow {R_{2b\min }} \Leftrightarrow {R_{b\min }} = 0 \Rightarrow {I_{1\max }} = \dfrac{U}{{{R_1}}} = \dfrac{{4,5}}{{15}} = 0,3A\)
+ Để \({I_{1\min }} \Leftrightarrow {R_{td\max }} \Leftrightarrow {R_{2b\max }} \Leftrightarrow {R_{b\max }} = 30\Omega \)
\(\begin{array}{l} \Rightarrow {R_{2b}}\, = \dfrac{{{R_2}{R_{b\max }}}}{{{R_2} + {R_{b\max }}}} = \dfrac{{10.30}}{{10 + 30}} = 7,5\Omega \\ \Rightarrow {I_{1\min }} = \dfrac{U}{{{R_1} + {R_{2b}}}} = \dfrac{{4,5}}{{15 + 7,5}} = 0,2A\end{array}\)
Hướng dẫn giải:
Công thức tính điện trở của mạch nối tiếp và song song: \(\left\{ \begin{array}{l}{R_{nt}} = {R_1} + {R_2}\\{R_{//}} = \dfrac{{{R_1}{R_2}}}{{{R_1} + {R_2}}}\end{array} \right.\)
Cường độ dòng điện chạy trong mạch: \(I = \dfrac{U}{{{R_{td}}}} \Rightarrow \left\{ \begin{array}{l}{I_{\max }} \Leftrightarrow {R_{td\min }}\\{I_{\min }} \Leftrightarrow {R_{td\max }}\end{array} \right.\)
Câu hỏi khác
- Bài tập định luật ôm cho đoạn mạch có các điện trở mắc nối tiếp lý 9 có lời giải
- Bài tập điện trở dây dẫn phụ thuộc vào các yếu tố của dây lý 9 có lời giải
- Bài tập định luật ôm cho đoạn mạch có các điện trở mắc song song lý 9 có lời giải
- Bài tập định luật ôm - điện trở của dây dẫn lý 9 có lời giải
- Bài tập biến trở - điện trở dùng trong kĩ thuật lý 9 có lời giải
