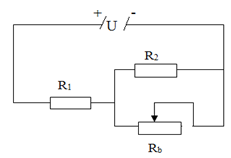
Một biến trở \({R_b}\) có giá trị lớn nhất là \(30\,\,\Omega \) được mắc với hai điện trở \({R_1} = 15\,\,\Omega \) và \({R_2} = 10\,\,\Omega \) thành mạch có sơ đồ như hình vẽ, trong đó hiệu điện thế không đổi \(U = 45\,\,V\). Hỏi khi điều chỉnh biến trở thì cường độ dòng điện chạy qua điện trở \({R_1}\) có giá trị lớn nhất \({I_{\max }}\) và nhỏ nhất \({I_{\min }}\) là bao nhiêu?

Cấu tạo mạch điện: \({R_1}nt\left( {{R_2}//{R_b}} \right)\)

Đặt \({R_x} = x\,\,\left( {0 \le x \le 30} \right)\)

Điện trở tương đương của mạch điện là:

\(R = {R_1} + \dfrac{{{R_2}.{R_x}}}{{{R_2} + {R_x}}} = 15 + \dfrac{{10x}}{{10 + x}} = 25 - \dfrac{{100}}{{x + 10}}\)

Cường độ dòng điện qua điện trở R₁ là:

\({I_1} = {I_m} = \dfrac{U}{R} = \dfrac{{45}}{{25 - \dfrac{{100}}{{x + 10}}}}\)

Để \({I_{1\max }} \Rightarrow {\left( {\dfrac{{45}}{{25 - \dfrac{{100}}{{x + 10}}}}} \right)_{\max }} \Rightarrow {\left( {25 - \dfrac{{100}}{{x + 10}}} \right)_{\min }}\)

\(\begin{array}{l} \Rightarrow {\left( { - \dfrac{{100}}{{x + 10}}} \right)_{\min }} \Rightarrow {\left( {\dfrac{{100}}{{x + 10}}} \right)_{\max }} \Rightarrow {\left( {x + 10} \right)_{\min }} \Rightarrow {x_{\min }} = 0\\ \Rightarrow {I_{1\max }} = \dfrac{{45}}{{25 - \dfrac{{100}}{{10}}}} = 3\,\,\left( A \right)\end{array}\)

Tương tự, để \({I_{1\min }} \Rightarrow {x_{\max }} = 30\,\,\left( \Omega  \right) \Rightarrow {I_{1\min }} = \dfrac{{45}}{{25 - \dfrac{{100}}{{30 + 10}}}} = 2\,\,\left( A \right)\)