Lúc $6$ giờ sáng, một người đi xe đạp từ A đến B với vận tốc $18$ km/giờ. Lúc $8$ giờ, một xe máy đi từ A đến B với vận tốc $45$ km/giờ. Hỏi xe máy đuổi kịp xe đạp vào lúc mấy giờ ? Địa điểm hai xe gặp nhau cách B bao xa? Biết rằng A cách B $115{\rm{ }}km$.
Trả lời bởi giáo viên
A. \(\,9\) giờ \(20\) phút; \(55km\)
Ta có sơ đồ chuyển động của hai xe như sau:
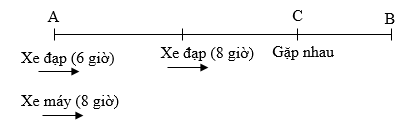
Thời gian xe đạp đi trước xe máy là:
\(8\) giờ $ - \,6$ giờ \( = \,2\) giờ
Quãng đường xe đạp đã đi trước khi xe máy xuất phát (hay khoảng cách giữa hai xe khi xe máy xuất phát) là:
\(18 \times 2 = 36\;(km)\)
Hiệu vận tốc hai xe là:
\(45 - 18 = 27\) (km/giờ)
Thời gian đi để xe máy đuổi kịp xe đạp là:
\(36:27 = \dfrac{4}{3}\) (giờ)
Đổi \(\dfrac{4}{3}\) giờ \( = \,1\dfrac{1}{3}\) giờ \( = \,\,1\) giờ \(20\) phút
Xe máy đuổi kịp xe đạp lúc:
$8$ giờ \( + \,1\) giờ \(20\) phút \( = \,9\) giờ \(20\) phút
Địa điểm gặp nhau cách A số ki-lô-mét là:
\(45 \times \dfrac{4}{3} = 60\;(km)\)
Địa điểm gặp nhau cách B số ki-lô-mét là:
\(115 - 60 = 55\;(km)\)
Đáp số: \(\,9\) giờ \(20\) phút; \(55km\).
Hướng dẫn giải:
Theo đề bài, xe đạp và xe máy xuất phát không cùng lúc. Đến $8$ giờ thì hai xe mới cùng chuyển động. Để giải bài này ta làm như sau:
- Tính thời gian xe đạp đi trước xe máy.
- Tìm quãng đường xe đạp đã đi trước khi xe máy xuất phát (hay khoảng cách giữa hai xe khi xe máy xuất phát) ta lấy vận tốc xe đạp nhân với thời gian xe đạp đi trước xe máy.
- Tìm hiệu vận tốc hai xe.
- Tìm thời gian đi để xe máy đuổi kịp xe đạp ta lấy khoảng cách giữa hai xe khi xe máy xuất phát chia cho hiệu vận tốc.
- Đổi số đo thời gian vừa tìm được sang số tự nhiên.
- Thời gian lúc xe máy đuổi kịp xe đạp = thời gian xuất phát của xe máy + thời gian đi để xe máy đuổi kịp xe đạp.
- Nếu số phút ở kết quả lớn hơn hoặc bằng \(60\) thì ta thực hiện chuyển đổi sang đơn vị lớn hơn phút là giờ.
- Tìm khoảng cách giữa điểm hai xe gặp nhau và B (đoạn đường BC) ta lấy độ dài quãng đường AB trừ đi khoảng cách từ A đến điểm hai xe gặp nhau (khoảng cách A đến điểm hai xe gặp nhau chính là quãng đường xe máy đi từ lúc xuất phát đến lúc gặp nhau, là đoạn đường AC).