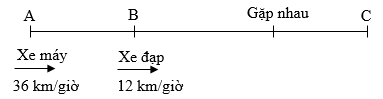
Lúc \(8\) giờ sáng, người thứ I đi từ A đi qua B để đến C với vận tốc $50$km/giờ. Cùng lúc đó tại B, người thứ II cũng khởi hành và đi cùng chiều với người thứ I với vận tốc $12$km/giờ. Biết rằng khoảng cách AB bằng $19km$. Hỏi hai người gặp nhau lúc mấy giờ?

Một ô tô đi từ A qua B để đi đến C với vận tốc là \({v_1}\), cùng lúc đó xe máy đi từ B đến C với vận tốc là \({v_2}\). Độ dài quãng đường AB là \(s\). Công thức tính thời gian đi để hai xe gặp nhau là:

Một người đi xe đạp từ B đến C với vận tốc \(12\) km/giờ, cùng lúc đó một người đi xe máy từ A cách B là \(60km\) với vận tốc \(36\) km/giờ và đuổi theo xe đạp (xem hình vẽ). Hỏi kể từ lúc bắt đầu đi, sau mấy giờ xe máy đuổi kịp xe đạp?

Điền số thích hợp vào ô trống:

Quân đi xe máy từ A đi qua B để đến C với vận tốc $40$ km/giờ. Cùng lúc đó tại B, Mai đi xe đạp và đi cùng chiều với Quân, với vận tốc $16$ km/giờ. Biết rằng khoảng cách AB bằng $36km$. Hỏi sau bao lâu hai người gặp nhau và địa điểm gặp nhau cách A bao nhiêu ki-lô-mét?

Điền số thích hợp vào ô trống:

Điền số thích hợp vào ô trống: