Lấy g = π2 = 10 m/s2. Treo con lắc đơn có độ dài ℓ = 100 cm trong thang máy, cho thang máy chuyển động nhanh dần đều đi lên với gia tốc a = 2 m/s2 thì chu kì dao động của con lắc đơn là:
Trả lời bởi giáo viên
+ Chu kì dao động của con lắc khi thang máy đứng yên: \(T = 2\pi \sqrt {\frac{l}{g}} \)
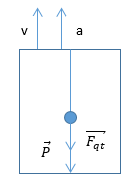
+ Khi thang máy đi lên nhanh dần đều => v,a hướng lên, Fqt hướng xuống
Chu kì dao động của con lắc khi đó:
\(T' = 2\pi \sqrt {\frac{l}{{g'}}} \)
\(\begin{array}{l}g' = g + a = 10 + 2 = 12m/{s^2}\\ \to \frac{{T'}}{T} = \sqrt {\frac{g}{{g'}}} = \sqrt {\frac{{10}}{{12}}} = 0,913 \to T' = 0,913T\end{array}\)
=> Chu kì T’ giảm 1 lượng bằng:
\(\frac{{\Delta T}}{T} = (1 - 0,913) = 0,087 = 8,7\% \)
Hướng dẫn giải:
+ Áp dụng công thức tính chu kì dao động của con lắc đơn: \(T = 2\pi \sqrt {\frac{l}{g}} \)
+ Áp dụng bài toán con lắc đơn chịu thêm tác dụng của lực quán tính

