Câu hỏi:
2 năm trước
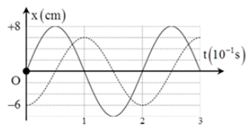
Hình vẽ bên là đồ thị biểu diễn sự phụ thuộc của li độ \(x\) vào thời gian \(t\) của hai dao động điều hòa cùng phương, cùng tần số. Dao động của vật là tổng hợp của hai dao động nói trên. Trong \(0,2s\) đầu tiên kể từ \(t = 0\), tốc độ trung bình của vật là
Trả lời bởi giáo viên
Đáp án đúng: d
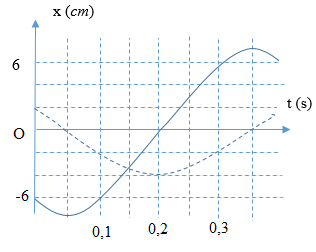
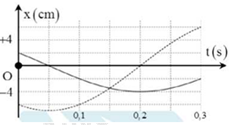
Từ đồ thị, ta có chu kì dao động là: \(T = 4.\left( {0,2 - 0,05} \right) = 0,6\,\,\left( s \right)\)
Tần số góc của dao động là: \(\omega = \dfrac{{2\pi }}{T} = \dfrac{{2\pi }}{{0,6}} = \dfrac{{10\pi }}{3}\,\,\left( {rad/s} \right)\)
Dao động thứ nhất có biên độ \({A_1} = 4\,\,\left( {cm} \right)\), tại \(t = 0\) li độ \({x_1} = 2\,\,\left( {cm} \right)\) và đang giảm, vậy phương trình dao động là \({x_1} = 4cos\left( {\dfrac{{10\pi }}{3}t + \dfrac{\pi }{3}} \right)\,\,\left( {cm} \right)\)
Dao động thứ 2, tại \(t = 0\) có li độ \({x_2} = - 6\,\,\left( {cm} \right)\), tại \(t = 0,2s\) là lần đầu vật qua vị trí cân bằng, nên ta có:
\(\dfrac{{10\pi }}{3}.0,2 + \varphi = - \dfrac{\pi }{2} \Rightarrow \varphi = - \dfrac{{7\pi }}{6}\left( {rad} \right)\)
\( \Rightarrow {A_2}cos\varphi = - 6 \Rightarrow {A_2} = \dfrac{{ - 6}}{{cos\varphi }} = \dfrac{{ - 6}}{{cos\left( { - \dfrac{{7\pi }}{6}} \right)}} = 4\sqrt 3 \,\,\left( {cm} \right)\)
Vậy dao động thứ 2 có phương trình dao động là: \({x_2} = 4\sqrt 3 cos\left( {\dfrac{{10\pi }}{3}t - \dfrac{{7\pi }}{6}} \right)\,\,\left( {cm} \right)\)
Phương trình dao động tổng hợp: \(x = {x_1} + {x_2} = 8cos\left( {\dfrac{{10\pi }}{3}t + \dfrac{{2\pi }}{3}} \right)cm\)
Vậy đến thời điểm \(t = 0,2\) thì vật ở vị trí có li độ là:
\(x = 8\cos \left( {\dfrac{{10\pi }}{3}.0,2 + \dfrac{{2\pi }}{3}} \right) = - 4\,\,\left( {cm} \right)\)
Trong \(0,2s\) đầu tiên kể từ \(t = 0\) vật đi được quãng đường là: \(S = 2.4 = 8\,\,\left( {cm} \right)\)
Vận tốc trung bình của vật là: \(v = \dfrac{8}{{0,2}} = 40\,\,\left( {cm/s} \right)\)
Hướng dẫn giải:
Sử dụng kĩ năng đọc đồ thị \(x - t\)
Viết phương trình dao động điều hòa của mỗi dao động
Tốc độ trung bình: \(v = \dfrac{s}{t}\)
Câu hỏi khác
- Bài tập lí thuyết dao động điều hòa có lời giải MÔN LÝ lớp 12
- Bài tập xác định thời gian vật chuyển động từ x1 đến x2, số lần qua li độ x có lời giải MÔN LÝ lớp 12
- Bài tập các đại lượng đặc trưng của DĐĐH có lời giải MÔN LÝ lớp 12
- Bài tập xác định quãng đường, tốc độ trung bình của vật trong DĐĐH có lời giải MÔN LÝ lớp 12
- Bài tập viết phương trình dao động điều hòa có lời giải MÔN LÝ lớp 12
