Hai nguồn sóng AB cách nhau \(90cm\) dao động cùng pha với bước sóng \(0,5m\). I là trung điểm AB. H là điểm nằm trên đường trung trực của AB cách I một đoạn \(15m\). Gọi d là đường thẳng qua H và song song với AB. Tìm điểm M thuộc d và gần H nhất, dao động với biên độ cực đại. (Tìm khoảng cách MH)
Trả lời bởi giáo viên
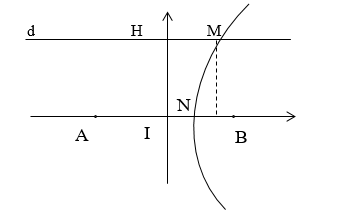
Cách 1:
+ Vì A và B cùng pha, do đó I dao động với biên độ cực đại.
Gọi N là giao của đường cực đại qua M và đường AB.
Vì M gần H nhất và dao động với biên độ cực đại nên
\(NI = \frac{\lambda }{2} = \frac{{0,5}}{2} = 0,25m\)
Theo tính chất về đường Hypecbol ta có:
Khoảng cách \(BI{\rm{ }} = {\rm{ }}c{\rm{ }} = 0,45m\)
Khoảng cách \(IN = a = 0,25m\)
Mà ta có \({b^2} + {\rm{ }}{a^2} = {\rm{ }}{c^2}\)
Suy ra \({b^2} = 0,14\)
Toạ độ điểm M là x, y thoả mãn: \(\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\)
Với \(x{\rm{ }} = {\rm{ }}MH,{\rm{ }}y{\rm{ }} = {\rm{ }}HI{\rm{ }} = 15m\)
\(\frac{{M{H^2}}}{{0,{{25}^2}}} - \frac{{{{15}^2}}}{{0,14}} = 1\)
Suy ra \(MH = 10,025m\)
Cách 2:
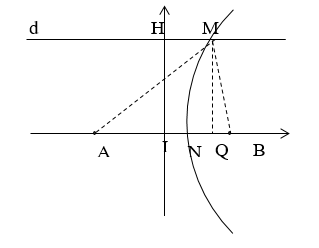
Vì A và B cùng pha và M gần H nhất và dao động với biên độ cực đại nên M thuộc cực đại ứng với k =1
Ta có: \(MA - MB = k\lambda = \lambda \)
Theo hình vẽ ta có: \(\sqrt {A{Q^2} + M{Q^2}} - \sqrt {B{Q^2} + M{Q^2}} = \lambda \)
Đặt \(MH{\rm{ }} = {\rm{ }}IQ{\rm{ }} = {\rm{ }}x\), có \(HI = MQ = 15m\)
Ta có: \(\sqrt {{{\left( {0,45 + x} \right)}^2} + {{15}^2}} - \sqrt {{{\left( {0,45 - x} \right)}^2} + {{15}^2}} = 0,5\)
(Dùng Shift Solve)
Giải phương trình tìm được \(x{\rm{ }} = {\rm{ }}10,025m\)
Hướng dẫn giải:
Áp dụng điều kiện dao động cực đại của 2 nguồn cùng pha: \({d_2} - {\rm{ }}{d_1} = {\rm{ }}k\lambda \)

