Câu hỏi:
2 năm trước
Gọi r và R lần lượt là bán kính đường tròn nội tiếp và ngoại tiếp của một tam giác đều. Tỷ số rR bằng:
Trả lời bởi giáo viên
Đáp án đúng: d
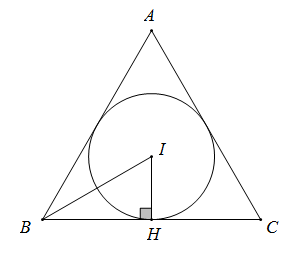
Giả sử tam giác đều ABC có đường tròn nội tiếp (I) tiếp xúc với BC tại H
⇒IH⊥BC
Vì ABC là tam giác đều nên I cũng là tâm đường tròn ngoại tiếp ∆ ABC
⇒IH là trung trực BC
⇒H là trung điểm BC
Vì I là tâm đường tròn nội tiếp tam giác nên BI là phân giác của ^ABC⇒^IBH=^ABC2=60∘2=30∘
Xét tam giác IHB ta có
rR=IHIB=sin^IBH=sin30∘=12
Hướng dẫn giải:
Sử dụng tỉ số lượng giác của góc nhọn để tính tỉ số cần thiết

