Trả lời bởi giáo viên
Đáp án đúng: a
log0,7(log6x2+xx+4)<0 .
Đkxđ: {log6x2+xx+4>0x2+xx+4>0⇔[−4<x<−2x>2(∗)
log6x2+xx+4>0,70=1⇔x2+xx+4>6⇔x2+xx+4−6>0⇔x2−5x−24x+4>0⇔(x−8)(x+3)x+4>0
Xét dấu f(x)=(x−8)(x+3)x+4:
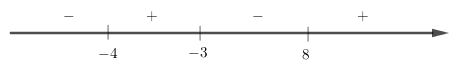
Vậy −4<x<−3 hoặc x>8.
Kết hợp với điều kiện ta được −4<x<−3 hoặc x>8.
Hướng dẫn giải:
Giải bất phương trình logarit cơ bản với chú ý về cơ số a>1 và 0<a<1.

