Câu hỏi:
2 năm trước
Đồ thị hàm số $y = {x^3} - 3x + 2$ có $2$ điểm cực trị $A,\;B.$ Diện tích tam giác $OAB\;$ với $O(0;0)$ là gốc tọa độ bằng:
Trả lời bởi giáo viên
Đáp án đúng: a
$\begin{array}{*{20}{l}}{y = {x^3} - 3x + 2 \Rightarrow y' = 3{x^2} - 3}\\{y' = 0 \Leftrightarrow x = {\rm{\;}} \pm 1}\end{array}$
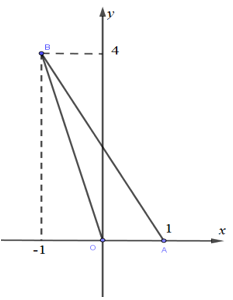
Tọa độ $2$ điểm cực trị : $A(1;{\mkern 1mu} 0),{\mkern 1mu} {\mkern 1mu} B( - 1;4)$
Khi đó ${S_{\Delta OAB}} = \dfrac{1}{2}.OA.{d(B,OA)} = \dfrac{1}{2}.\left| {{x_A}} \right|.\left| {{y_B}} \right| = \dfrac{1}{2}.\left| 1 \right|.\left| 4 \right| = 2$
Hướng dẫn giải:
- Xác định tọa độ 2 điểm cực trị $A,\;B.$
- Tính diện tích tam giác $OAB$ theo công thức: $S = \dfrac{1}{2}a.h$ (với $a$ là độ dài đáy, $h$ là độ dài đường cao tương ứng với đáy đã chọn).
Giải thích thêm:
Cách khác:
Tính $AB = \sqrt {{{( - 1 - 1)}^2} + {{(4 - 0)}^2}} = 2\sqrt 5 $
Lập phương trình đường thẳng $AB:$$2x + y - 2 = 0$$ \Rightarrow d(O,AB) = \dfrac{{\left| {2.0 + 0 - 2} \right|}}{{\sqrt {{2^2} + 1} }} = \dfrac{2}{{\sqrt 5 }}$
${S_{\Delta OAB}} = \dfrac{1}{2}.AB.d(O;AB) = \dfrac{1}{2}.2\sqrt 5 .\dfrac{2}{{\sqrt 5 }} = 2.$
Chọn A.
