Câu hỏi:
2 năm trước
Độ dài đường trung tuyến ứng với cạnh huyền của tam giác vuông có các cạnh góc vuông bằng \(5\,cm\), \(12\,cm\) là:
Trả lời bởi giáo viên
Đáp án đúng: a
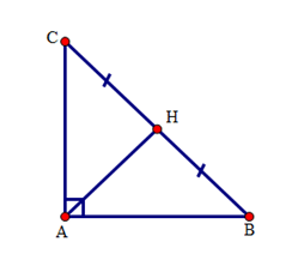
Áp dụng định lý Pytago cho tam giác \(ABC\) vuông tại \(A\) ta có:
\(B{C^2} = A{C^2} + A{B^2}\) hay \(B{C^2} = {5^2} + {12^2}\)\( \Rightarrow \)\(B{C^2} = 169\). Suy ra \(BC = 13\,\left( {cm} \right)\).
Do \(AH\) là đường trung tuyến ứng với cạnh huyền \(BC\) nên \(AH = BC:2 = 13:2 = 6,5\left( {cm} \right)\).
Hướng dẫn giải:
Bước 1: Áp dụng định lý Pytago để tính độ dài cạnh huyền.
Bước 2: Sử dụng tính chất trong tam giác vuông đường trung tuyến ứng với cạnh huyền bằng một nửa cạnh huyền để tính độ dài đường trung tuyến.