Đề thi THPT QG 2020 – mã đề 104

Cho hình chóp đều \(S.ABCD\) có tất cả các cạnh bằng \(a\) và \(O\) là tâm của đáy. Gọi \(M,N,P,Q\) lần lượt là các điểm đối xứng với \(O\) qua trọng tâm của các tam giác \(SAB,\,\,SBC,\,\,SCD,\,\,SDA\) và \(S'\) là điểm đối xứng với \(S\) qua \(O\). Thể tích khối chóp \(S'MNPQ\) bằng

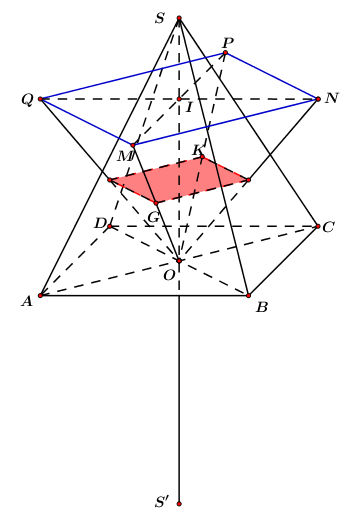
\(S.ABCD\) là hình chóp đều nên trọng tâm của các mặt bên tạo thành một hình vuông

=> MNPQ là hình vuông

Ta có : \(AC = a\sqrt 2 .\)

\( \Rightarrow SO = \sqrt {S{A^2} - A{O^2}}  = \sqrt {{a^2} - {{\left( {\dfrac{{a\sqrt 2 }}{2}} \right)}^2}}  = \dfrac{{a\sqrt 2 }}{2}\)

Gọi \(G,\,\,K\) lần lượt là trọng tâm của \(\Delta SAB\) và \(\Delta SCD\).

\( \Rightarrow GK = \dfrac{2}{3}BC = \dfrac{2}{3}a = \dfrac{{2a}}{3}.\)  (tính chất trọng tâm tam giác)

\( \Rightarrow MP = 2GK = \dfrac{4}{3}a\) (tính chất đường trung bình của tam giác)

Tương tự ta được: \(NQ = \dfrac{4}{3}a\).

\( \Rightarrow {S_{MNPQ}} = \dfrac{1}{2}MP.NQ = \dfrac{1}{2}.{\left( {\dfrac{4}{3}a} \right)^2} = \dfrac{8}{9}{a^2}\) .

Ta có: \(\left( {MNPQ} \right){\rm{//}}\left( {ABCD} \right)\)

\( \Rightarrow d\left( {M,\left( {ABCD} \right)} \right) = 2d\left( {G,\left( {ABCD} \right)} \right)\)\( = \dfrac{2}{3}SO = \dfrac{{a\sqrt 2 }}{3}\).

\( \Rightarrow d\left( {\left( {MNPQ} \right),\left( {ABCD} \right)} \right) = \dfrac{{a\sqrt 2 }}{3}\)

\( \Rightarrow d\left( {S',\left( {MNPQ} \right)} \right) = S'O + \dfrac{{a\sqrt 2 }}{3} = \dfrac{{5a\sqrt 2 }}{6}\)

\( \Rightarrow {V_{S'MNPQ}} = \dfrac{1}{3}.\dfrac{{5a\sqrt 2 }}{6}.\dfrac{{8{a^2}}}{9} = \dfrac{{20\sqrt 2 {a^3}}}{{81}}\).