Đề thi THPT QG 2020 – mã đề 104

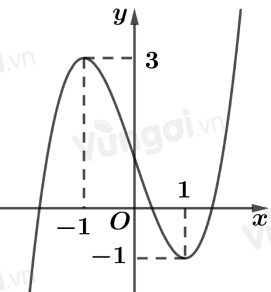
Cho hàm số bậc bốn \(f\left( x \right)\) có bảng biến thiên như sau

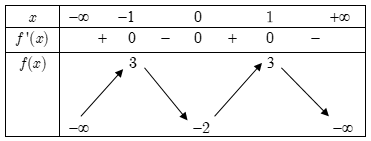
Số điểm cực trị của hàm số \(g(x) = {x^2}{\left[ {f(x + 1)} \right]^4}\)

Ta có: \(g\left( x \right) = {x^2}{\left[ {f\left( {x + 1} \right)} \right]^4}\)

\( \Rightarrow g'\left( x \right) = 2x{\left[ {f\left( {x + 1} \right)} \right]^4} + 4{x^2}{\left[ {f\left( {x + 1} \right)} \right]^3}.f'\left( {x + 1} \right)\) \( = 2x{\left[ {f\left( {x + 1} \right)} \right]^3}\left[ {f\left( {x + 1} \right) + 2x.f'\left( {x + 1} \right)} \right].\)

\(\begin{array}{l} \Rightarrow g'\left( x \right) = 0\\ \Leftrightarrow 2x{\left[ {f\left( {x + 1} \right)} \right]^3}\left[ {f\left( {x + 1} \right) + 2x.f'\left( {x + 1} \right)} \right] = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = 0\\f\left( {x + 1} \right) = 0\,\,\,\,\,\,\,\left( 1 \right)\\f\left( {x + 1} \right) + 2x.f'\left( {x + 1} \right) = 0\,\,\,\,\,\,\left( 2 \right)\end{array} \right.\end{array}\)

+) Xét phương trình \(\left( 1 \right)\) ta có:

\(f\left( {x + 1} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = {x_1} <  - 2\\x = {x_2} \in \left( { - 2; - 1} \right)\\x = {x_3} \in \left( { - 1;\,\,0} \right)\\x = {x_4} > 0\end{array} \right.\)

+) Xét phương trình \(\left( 2 \right)\)  ta có: \(f\left( {x + 1} \right) + 2x.f'\left( {x + 1} \right) = 0\)

\( \Leftrightarrow f\left( {x + 1} \right) + 2\left( {x + 1} \right).f'\left( {x + 1} \right) - 2f'\left( {x + 1} \right) = 0\,\,\,\left( * \right)\)

Đặt \(h\left( x \right) = f\left( {x + 1} \right) + 2\left( {x + 1} \right).f'\left( {x + 1} \right) - 2f'\left( {x + 1} \right)\)

Đặt \(t = x + 1\) ta được: \(h\left( t \right) = f\left( t \right) + 2t.f'\left( t \right) - 2f'\left( t \right).\)

\( \Rightarrow \left( * \right) \Leftrightarrow f\left( t \right) + 2t.f'\left( t \right) - 2f'\left( t \right) = 0\,\,\,\,\left( {**} \right)\)

Dựa vào BBT ta thấy hàm số \(y = f\left( x \right)\) có dạng: \(f\left( x \right) = a{x^4} + b{x^2} + c\)

\( \Rightarrow f'\left( x \right) = 4a{x^3} + 2bx\)

Ta thấy hàm số có 2 điểm cực đại \(\left( { - 1;\,\,3} \right),\,\,\left( {1;\,\,3} \right)\), 1 điểm cực trị \(\left( {0; - 2} \right)\) nên ta có:

\(\left\{ \begin{array}{l}c =  - 2\\4a + 2b = 0\\a + b + c = 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a =  - 5\\b = 10\\c =  - 2\end{array} \right.\) \( \Rightarrow f\left( x \right) =  - 5{x^4} + 10{x^2} - 2\)\( \Rightarrow f'\left( x \right) =  - 20{x^3} + 20x.\)

\(\begin{array}{l} \Rightarrow \left( {**} \right) \Leftrightarrow  - 5{t^4} + 10{t^2} - 2 + 2t\left( { - 20{t^3} + 20t} \right) - 2\left( { - 20{t^3} + 20t} \right) = 0\\ \Leftrightarrow  - 5{t^4} + 10{t^2} - 2 - 40{t^4} + 40{t^2} + 40{t^3} - 40t = 0\\ \Leftrightarrow  - 45{t^4} + 40{t^3} + 50{t^2} - 40t - 2 = 0\,\,\,\,\left( {***} \right)\end{array}\)

Lập bảng biến thiên ta được phương trình \(\left( {***} \right)\) có 4 nghiệm \(t\)

\( \Rightarrow \left( 2 \right)\) có 4 nghiệm \(x.\)

\( \Rightarrow g'\left( x \right) = 0\) có 9 nghiệm phân biệt.

\( \Rightarrow \) Hàm số \(g\left( x \right)\) có 9 điểm cực trị.