Trả lời bởi giáo viên
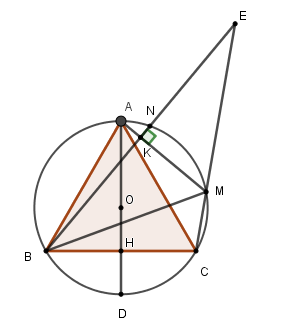
Xét đường tròn \(\left( O \right)\) có tam giác \(ABC\) đều nên sđ \(\overparen{AB} = sđ\overparen{AC} \)\(= sđ\overparen{BC} = \dfrac{{360^\circ }}{3} = 120^\circ \)
\(\widehat {AMB}\) là góc nội tiếp chắn cung \(AB\)\( \Rightarrow \widehat {AMB} = \dfrac{1}{2}sđ\overparen{AB}\)\( = \dfrac{{120^\circ }}{2} = 60^\circ \)
Suy ra \(\widehat {KBM} = 90^\circ - \widehat {KMB}\)\( = 90^\circ - 60^\circ = 30^\circ \) suy ra \(sđ\overparen{NM} = 2.\widehat {NBM} = 2.30^\circ = 60^\circ \)
\(\widehat {NBM} = 30^\circ \left( {cmt} \right)\) và \(\widehat {BEM} = \dfrac{1}{2}\left( {sđ\overparen{BC} - sđ\overparen{NM}} \right) \)\(= \dfrac{1}{2}\left( {120^\circ - 60^\circ } \right) = 30^\circ \) nên tam giác \(MBE\) cân tại \(M.\)
Hướng dẫn giải:
Chứng minh tam giác \(MBE\) có hai góc ở đáy bằng nhau
Sử dụng:
+ Số đo góc nội tiếp bằng nửa số đo cung bị chắn
+ Góc có đỉnh bên ngoài đường tròn bằng nửa hiệu số đo hai cung bị chắn

