Trả lời bởi giáo viên
Đáp án đúng: d
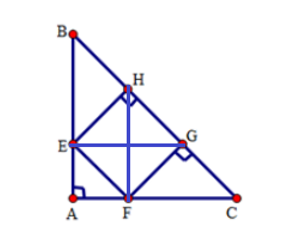
Ta có: ΔABC vuông cân tại A nên ˆB=ˆC=180∘−ˆA2=180∘−90∘2=45∘.
Xét tam giác vuông FGC có:
^GFC=180∘−^FGC−ˆC=180∘−90∘−45∘=45∘ ⇒^GFC=ˆC.
Suy ra: ΔFGC là tam giác vuông cân tại G ⇒FG=GC.
Chứng minh tương tự:
Xét tam giác vuông EHB có: ^BEH=180∘−^EHB−ˆB=180∘−90∘−45∘=45∘⇒^BEH=ˆB.
Suy ra tam giác EBH vuông cân tại H ⇒EH=HB.
Mà BH=HG=GC(gt) nên FG=EH=HG.
Lại có: EH⊥BC(gt)FG⊥BC(gt)}⇒EH//FG (định lí từ vuông góc đến song song)
Xét tứ giác EFGH có:
{EH=FG(cmt)EH//FG(cmt) ⇒ Tứ giác EFGH là hình bình hành (dhnb).
Mà ˆH=90∘ (do EH⊥BC) nên hình bình hành EFGH là hình chữ nhật.
Mặt khác: EH=HG(cmt) nên hình chữ nhật EFGH là hình vuông.
Suy ra: EG=HF;EG⊥HF.
Hướng dẫn giải:
Sử dụng dấu hiệu nhận biết hình bình hành, hình chữ nhật, hình vuông.
Sử dụng tính chất hình vuông.

