Trả lời bởi giáo viên
Đáp án đúng: d
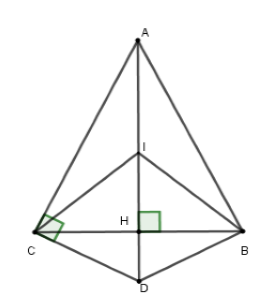
Ta có ΔABC cân tại A có đường cao AH nên AH cũng là đường phân giác ⇒^CAD=^DAB
Suy ra ΔACD=ΔABD(c−g−c) nên ^ABD=^ACD=90∘ và CD=DB nên A, B đúng.
Lấy I là trung điểm AD. Xét hai tam giác vuông ABD và ACD có IA=ID=IB=IC=AD2
Nên I là điểm cách đều A,B,D,C hay A,B,D,C cùng nằm trên dường tròn tâm I đường kính AD nên đáp án C đúng.
Hướng dẫn giải:
+ Chứng minh hai tam giác bằng nhau để suy ra cặp cạnh bằng nhau
+ Xác định điểm cách đều cả bốn đỉnh cho trước, điểm đó chính là tâm đường tròn đi qua 4 đỉnh.
Câu hỏi khác
- Bài tập tính chất hai tiếp tuyến cắt nhau toán 9 có lời giải
- Bài tập sự xác định của đường tròn- tính chất đối xứng của đường tròn toán 9 có lời giải
- Bài tập vị trí tương đối giữa đường thẳng và đường tròn toán 9 có lời giải
- Bài tập đường kính và dây của đường tròn toán 9 có lời giải
- Bài tập dấu hiệu nhận biết tiếp tuyến của đường tròn toán 9 có lời giải
