Cho tứ giác $ABCD.$ Gọi $M,{\rm{ }}N,{\rm{ }}P,{\rm{ }}Q$ lần lượt là trung điểm các cạnh $AB,{\rm{ }}BC,{\rm{ }}CD,{\rm{ }}DA.$ Hai đường chéo $AC$ và $BD$ phải thỏa mãn điều kiện gì để $M,{\rm{ }}N,{\rm{ }}P,{\rm{ }}Q$ là bốn đỉnh của hình vuông.

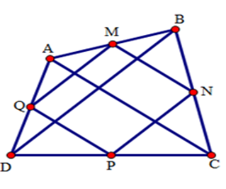
Xét tam giác $ABD$ có:

$M$ là trung điểm của $AB$ (gt)

$Q$ là trung điểm của $AD$   (gt)

\( \Rightarrow \) $QM$ là đường trung bình của tam giác $ABD.$ (định lý)

Do đó $QM//BD$ và \(QM = \dfrac{1}{2}BD\) (1)

Tương tự ta cũng có $NP$ là đường trung bình của tam giác $BCD.$

 \( \Rightarrow \left\{ \begin{array}{l}NP//BD\\NP = \dfrac{1}{2}BD\,\,\,\,\left( 2 \right)\end{array} \right.\) 

Từ (1) và (2) ta suy ra $MNPQ$ là hình bình hành (dấu hiệu nhận biết).

Tương tự ta cũng có $MN$ là đường trung bình của tam giác $BAC$ nên $MN//AC$ và \(MN = \dfrac{1}{2}AC\)

Để hình bình hành $MNPQ$ là hình vuông \( \Leftrightarrow \left\{ \begin{array}{l}MN \bot NP\\MN = NP\end{array} \right.\)

+ Để \(MN \bot NP \Leftrightarrow AC \bot BD\) (vì $MN//AC,{\rm{ }}NP//BD$ )

+  Để \(MN = NP \Leftrightarrow AC = BD\) (vì \(MN = \dfrac{1}{2}AC,NP = \dfrac{1}{2}BD\) )

Vậy điều kiện cần tìm để $MNPQ$ là hình vuông là \(BD = AC;BD \bot AC.\) .