Cho tứ diện $ABCD$ có \(AB = a\), $CD = b$. Gọi \(I\), \(J\) lần lượt là trung điểm \(AB\) và \(CD\), giả sử \(AB \bot CD\). Mặt phẳng $\left( \alpha  \right)$ qua $M$ nằm trên đoạn $IJ$ và song song với \(AB\) và \(CD\). Tính diện tích thiết diện của tứ diện $ABCD$ với mặt phẳng $\left( \alpha  \right)$ biết $IM = \dfrac{1}{3}IJ$.

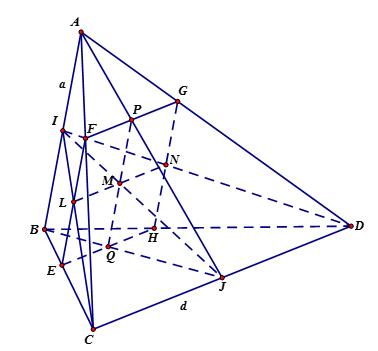
Ta có $\left\{ \begin{array}{l}\left( \alpha  \right){\rm{// }}CD\\CD \subset \left( {ICD} \right)\\M \in \left( \alpha  \right) \cap \left( {ICD} \right)\end{array} \right.$$ \Rightarrow $ giao tuyến của $\left( \alpha  \right)$ với $\left( {ICD} \right)$ là đường thẳng qua $M$ và

song song với $CD$cắt $IC$ tại $L$ và $ID$ tại $N$.

$\left\{ \begin{array}{l}\left( \alpha  \right){\rm{// }}AB\\AB \subset \left( {JAB} \right)\\M \in \left( \alpha  \right) \cap \left( {JAB} \right)\end{array} \right.$$ \Rightarrow $ giao tuyến của $\left( \alpha  \right)$ với $\left( {JAB} \right)$ là đường thẳng qua $M$ và song song

với $AB$cắt $JA$ tại $P$ và $JB$ tại $Q$.

Ta có $\left\{ \begin{array}{l}\left( \alpha  \right){\rm{// }}AB\\AB \subset \left( {ABC} \right)\\L \in \left( \alpha  \right) \cap \left( {ABC} \right)\end{array} \right.$$ \Rightarrow EF{\rm{// }}AB$  (1)

Tương tự $\left\{ \begin{array}{l}\left( \alpha  \right){\rm{// }}AB\\AB \subset \left( {ABD} \right)\\N \in \left( \alpha  \right) \cap \left( {ABD} \right)\end{array} \right.$$ \Rightarrow HG{\rm{// }}AB$  (2).

Từ  (1) và (2) $ \Rightarrow EF{\rm{// }}HG{\rm{// }}AB$ (3)

Ta có $\left\{ \begin{array}{l}\left( \alpha  \right){\rm{// }}CD\\CD \subset \left( {ACD} \right)\\P \in \left( \alpha  \right) \cap \left( {ACD} \right)\end{array} \right.$$ \Rightarrow FG{\rm{// }}CD$  (4) 

Tương tự $\left\{ \begin{array}{l}\left( \alpha  \right){\rm{// }}CD\\CD \subset \left( {BCD} \right)\\Q \in \left( \alpha  \right) \cap \left( {BCD} \right)\end{array} \right.$$ \Rightarrow EH{\rm{// }}CD$  (5)            

Từ  (4) và (5) $ \Rightarrow FG{\rm{// }}EH{\rm{// }}CD$ (6).

Từ  (3) và (6), suy ra $EFGH$ là hình  bình hành. Mà \(AB \bot CD\) nên $EFGH$ là hình chữ nhật.

Xét tam giác $ICD$có: $LN{\rm{// }}CD$ $ \Rightarrow \dfrac{{LN}}{{CD}} = \dfrac{{IN}}{{ID}}$ .

Xét tam giác $ICD$ có: $MN{\rm{// }}JD$ $ \Rightarrow \dfrac{{IN}}{{ID}} = \dfrac{{IM}}{{IJ}}$ .

Do đó $\dfrac{{LN}}{{CD}} = \dfrac{{IM}}{{IJ}} = \dfrac{1}{3}$$ \Rightarrow LN = \dfrac{1}{3}CD = \dfrac{b}{3}$.

Tương tự $\dfrac{{PQ}}{{AB}} = \dfrac{{JM}}{{JI}} = \dfrac{2}{3}$$ \Rightarrow PQ = \dfrac{2}{3}AB = \dfrac{{2a}}{3}$.     

Vậy ${S_{EFGH}} = PQ.LN = \dfrac{{2ab}}{9}$.