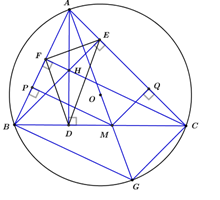
Cho tam giác nhọn \(ABC\;\left( {AB < AC} \right)\) nội tiếp đường tròn tâm \(O\), có ba đường cao là \(AD,BE,CF\) và trực tâm là \(H\). Gọi \(M\)là giao điểm của \(AO\) với \(BC\) và \(P,\;Q\)lần lượt là chân các đường vuông góc kẻ từ \(M\) đến \(AB,AC\).

Chọn câu đúng.

:   \(\)   

*)  Xét tứ giác \(HDCE\) có: \(\left\{ \begin{array}{l}\angle HEC = {90^o}\\\angle HDC = {90^o}\end{array} \right. \Rightarrow \angle HEC + \angle HDC = {180^o}\)

Suy ra tứ giác \(HDCE\) nội tiếp đường tròn \( \Rightarrow \angle HDE = \angle HCE\) ( 2 góc nội tiếp cùng chắn cung \(HE\))

Chứng minh tương tự có \(\angle FBH = \angle FDH\)

Mà có \(\angle FBH = \angle HCE\) (do cùng phụ với \(\angle BAC\))

\( \Rightarrow \angle FDH = \angle HDE\) , suy ra \(HD\) là phân giác \(\angle FDE\)

Chứng minh tương tự ta có : \(HE\)là tia phân giác \(\angle FED\) ; \(FH\) là phân giác \(\angle DFE\)

Suy ra H là giao của 3 đường phân giác trong \(\Delta FDE\) , suy ra H là tâm đường tròn nội tiếp \(\Delta FDE\;\;\left( {dpcm} \right).\)

*) Kéo dài \(AO\) cắt \(\left( O \right)\) tại \(G.\)

Có\(\angle ACG = {90^o}\)(góc nội tiếp chắn nửa đường tròn)

Suy ra \(BH//GC\) (do cùng vuông góc với ${\rm{AC}}$)

Chứng minh tương tự có \(HC//BG\)

\( \Rightarrow BHCG\) là hình bình hành  (do có 2 cặp cạnh đối song song)\( \Rightarrow \left\{ \begin{array}{l}BH = GC\\HC = BG\end{array} \right.\)

Xét \(\Delta ACG\) có : \(MQ//GC\) (do cùng vuông góc với ${\rm{AC}}$)

\( \Rightarrow \dfrac{{MQ}}{{GC}} = \dfrac{{AM}}{{AG}}\) (định lí Ta-lét)

Chứng minh tương tự có \(\dfrac{{PM}}{{BG}} = \dfrac{{AM}}{{AG}}\)

\(\)\( \Rightarrow \dfrac{{MQ}}{{GC}} = \dfrac{{PM}}{{BG}}\left( { = \dfrac{{AM}}{{AG}}} \right).\)

Mà có \(\left\{ \begin{array}{l}BH = GC\\HC = BG\end{array} \right. \Rightarrow \dfrac{{MQ}}{{BH}} = \dfrac{{PM}}{{HC}} \Rightarrow \dfrac{{MQ}}{{PM}} = \dfrac{{BH}}{{HC}}\;\;\;\;\;\;\left( 1 \right)\) \(\)

Xét \(\Delta FHB\) và \(\Delta EHC\) có:

 \(\angle FBH = \angle HCE\)  (do cùng phụ với \(\angle BAC\))

\(\angle BFH = \angle HEC = {90^o}\)

\( \Rightarrow \Delta FHB \backsim \Delta EHC\left( {g - g} \right) \Rightarrow \dfrac{{FH}}{{HE}} = \dfrac{{BH}}{{HC}}\)        (2)\(\)   \(\)

Từ (1) và (2) \( \Rightarrow \dfrac{{MQ}}{{PM}} = \dfrac{{FH}}{{HE}} \Rightarrow MQ.HE = HF.MP.\)

Vậy cả A, B đều đúng.