Câu hỏi:
3 năm trước
Cho tam giác $ABC,$ đường cao $AH$ . Gọi $I$ là trung điểm của $AC,E$ là điểm đối xứng với $H$ qua $I$. Tứ giác $AECH$ là hình gì?
Trả lời bởi giáo viên
Đáp án đúng: a
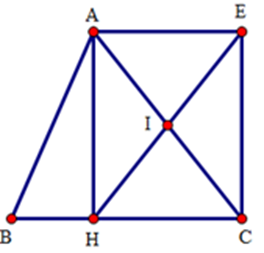
Xét tứ giác $AECH$ có: $I$ là trung điểm của $AC$ (gt); $I$ là trung điểm của $HE$ (do $H$ và $E$ đối xứng nhau qua $I$ )
Do đó $AECH$ là hình bình hành (dấu hiệu nhận biết).
Lại có \(\widehat {AHC} = {90^ \circ }\) , nên $AECH$ là hình chữ nhật (dhnb).
Hướng dẫn giải:
+ Chứng minh $AECH$ là hình bình hành dựa vào dấu hiệu tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường là hình bình hành.
+ Chứng minh hình bình hành $AECH$ là hình chữ nhật dựa vào dấu hiệu hình bình hành có một góc vuông là hình chữ nhật.

