Câu hỏi:
2 năm trước
Cho tam giác \(ABC\), điểm \(D\) thuộc cạnh \(AC\) sao cho \(AD = \dfrac{1}{2}DC\). Gọi \(M\) là trung điểm của \(BC,I\) là giao điểm của \(BD\) và \(AM\). Tính \(AM\) biết \(IM = 3\,cm\).
Trả lời bởi giáo viên
Đáp án đúng: b
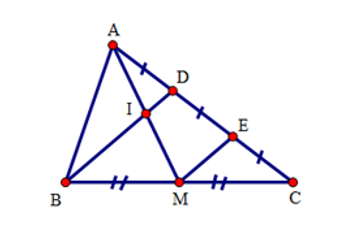
Gọi \(E\) là trung điểm của \(DC\).
Xét tam giác \(BDC\) có: \(BM = MC,DE = EC\) nên \(ME\) là đường trung bình của tam giác\(BDC\) . Suy ra \(BD//ME\) hay \(DI//EM\).
Xét tam giác \(AME\) có \(AD = DE,DI//EM\) nên \(AI\; = IM\).
Suy ra \(AM = 2IM = 2.3 = 6\,cm\).
Hướng dẫn giải:
Sử dụng dấu hiệu nhận biết để chứng minh các đoạn thẳng là đường trung bình của tam giác. Từ đó dùng các định lý của đường trung bình để suy ra điều cần chứng minh.