Cho tam giác \(ABC\) có \(M\) là trung điểm của \(BC\) và \(AM = \dfrac{{BC}}{2}\). Số đo góc \(BAC\) là
Trả lời bởi giáo viên
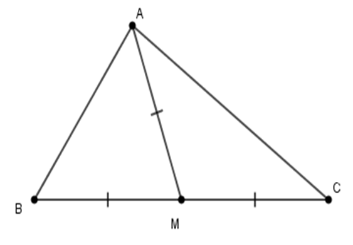
Từ giả thiết suy ra \(AM = BM = CM\)
Ta có \(\widehat {BAC} + \widehat B + \widehat C = 180^\circ \) (định lý tổng ba góc trong tam giác) (1)
Lại có \(\Delta AMB\) cân tại \(M\,\left( {{\rm{do}}\,\,MA = MB} \right)\) nên \(\widehat B = \widehat {BAM}\) (tính chất) (2)
Tương tự \(\Delta AMC\) cân tại \(M\,\left( {{\mathop{\rm do}\nolimits} \,\,MA = MC} \right)\) nên \(\widehat C = \widehat {MAC}\) (tính chất) (3)
Từ (1); (2); (3) ta có \(\widehat {BAC} + \widehat {BAM} + \widehat {CAM} = 180^\circ \) \( \Rightarrow \widehat {BAC} + \widehat {BAC} = 180^\circ \) \(2.\widehat {BAC} = 180^\circ \) \( \Rightarrow \widehat {BAC} = 90^\circ .\)
Hướng dẫn giải:
Dựa vào tính chất tổng các góc của tam giác và dựa vào tính chất tam giác cân.

