Câu hỏi:
3 năm trước
Cho tam giác \(ABC\) có \(AC > AB.\) Trên cạnh \(AC\) lấy điểm \(E\) sao cho \(CE = AB.\) Các đường trung trực của \(BE\) và \(AC\) cắt nhau tại \(O.\)
Chọn câu đúng
Trả lời bởi giáo viên
Đáp án đúng: d
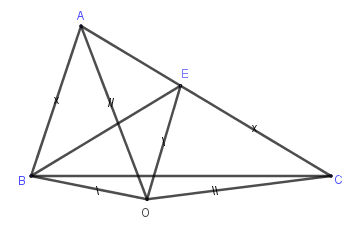
Ta có \(\Delta AOB = \Delta COE \Rightarrow \widehat {OAB} = \widehat {OCE}\,\,\left( 1 \right)\)
\(\Delta AOC\) cân tại \(O \Rightarrow \widehat {OAC} = \widehat {OCE}\,\,\left( 2 \right)\)
Từ \(\left( 1 \right);\left( 2 \right)\) suy ra \(\widehat {OAB} = \widehat {OAC}\) , do đó \(AO\) là tia phân giác góc \(A.\)
Hướng dẫn giải:
+ Sử dụng tính chất hai tam giác bằng nhau và định nghĩa đường phân giác của một góc

