Cho tam giác \(ABC\) có \(\widehat A\) là góc tù. Tia phân giác của góc \(B\) và góc \(C\) cắt nhau tại \(O.\) Lấy điểm \(E\) trên cạnh \(AB.\) Từ \(E\) kẻ \(EP \bot BO\,\,\left( {P \in BC} \right).\) Từ \(P\) kẻ \(PF \bot OC\,\left( {F \in AC} \right).\)

Chọn câu đúng.

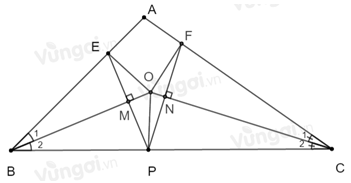
Giả sử \(EP \bot BO\) tại \(M\); \(PF \bot OC\) tại \(N\).

Khi đó \(\widehat {BME} = \widehat {BMP} = {90^0}\); \(\widehat {CNF} = \widehat {PNC} = {90^0}\)

Vì \(BO\) là tia phân giác của \(\widehat {ABC}\) (gt) nên \(\widehat {{B_1}} = \widehat {{B_2}}\) (tính chất tia phân giác)

Xét \(\Delta BME\) và \(\Delta BMP\) có:

\(\widehat {BME} = \widehat {BMP} = {90^0}\) (cmt)

\(BM\) là cạnh chung

\(\widehat {{B_1}} = \widehat {{B_2}}\) (cmt)

Do đó \(\Delta BME = \Delta BMP\) (g.c.g) suy ra \(ME = MP\) (hai cạnh tương ứng)

Mặt khác: \(EP \bot BO\) (gt)

Vậy \(OB\) là đường trung trực của đoạn \(EP\) (định nghĩa đường trung trực của đoạn thẳng). Đáp án A đúng.

Chứng minh tương tự ta có: \(\Delta CNF = \Delta CNP\) (g.c.g) suy ra \(NF = NP\) (hai cạnh tương ứng)

Mặt khác \(PF \bot OC\) (gt)

Vậy \(OC\) là đường trung trực của đoạn \(PF\) (định nghĩa đường trung trực của đoạn thẳng). Đáp án B đúng