Cho tam giác \(ABC\) cân tại \(B,\,\widehat {BAC} = {80^0}.\) Lấy \(I\) là điểm nằm trong tam giác sao cho \(\widehat {IAC} = {10^0};\widehat {ICA} = {30^0}.\) Tính góc \(ABI.\)

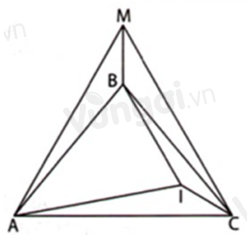
Trên nửa mặt phẳng bờ \(AC\) chứa điểm \(B\) lấy điểm \(M\) sao cho \(\Delta ACM\) đều.

Xét \(\Delta AMB\) và \(\Delta CMB\) có:

\(BM\) cạnh chung

\(AM = CM\) (vì \(\Delta ACM\) đều)

\(AB = CB\) (vì \(\Delta ABC\) cân tại \(B\))

\( \Rightarrow \Delta AMB = \Delta CMB\,(c.c.c)\)

\( \Rightarrow \widehat {AMB} = \widehat {CMB}\) (hai góc tương ứng)       (1)

Mà \(\widehat {AMB} + \widehat {CMB} = \widehat {ABC} = {60^o}\) (vì \(\Delta ACM\) đều)     (2)

Từ (1) và (2) suy ra: \(\widehat {AMB} = \widehat {CMB} = \dfrac{{{{60}^o}}}{2} = {30^o}\)

\(\Delta ABC\) cân tại \(B\) nên \(\widehat {BAC} = \widehat {BCA} = \dfrac{{{{180}^o} - \widehat {ABC}}}{2} = \dfrac{{{{180}^o} - {{80}^o}}}{2} = {50^o}\).

Ta có: \(\widehat {CAB} + \widehat {BAM} = \widehat {CAM} = {60^o}\) (vì \(\Delta ACM\) đều)

\( \Rightarrow \widehat {BAM} = {60^o} - \widehat {CAB} = {60^o} - {50^o} = {10^o}\)

Xét \(\Delta AMB\) và \(\Delta ACI\) có:

\(AM = AC\) (vì \(\Delta ACM\) đều)

\(\widehat {BAM} = \widehat {IAC} = {10^o}\)

\(\widehat {AMB} = \widehat {ACI} = {30^o}\)

\( \Rightarrow \Delta AMB = \Delta ACI\,(g.c.g)\)

\( \Rightarrow AB = AI\) (hai cạnh tương ứng)

Do đó \(\Delta ABI\) cân tại \(A\).

Ta có: \(\widehat {BAI} = \widehat {BAC} - \widehat {IAC} = {50^o} - {10^o} = {40^o}\)

\(\Delta ABI\) cân tại \(A\) nên \(\widehat {ABI} = \dfrac{{{{180}^o} - \widehat {BAI}}}{2} = \dfrac{{{{180}^o} - {{40}^o}}}{2} = {70^o}.\)